Задача 1406 а) Решите уравнение...

slava191

03.06.2014

а) Решите уравнение 7sin^2x+4sinxcosx-3cos^2x=0
б) Укажите корни, принадлежащие промежутку [3Pi/2;5Pi/2].

P.S. Это тригонометрическое уравнение из ЕГЭ по Математике. Разбор таких задач можно посмотреть здесь: [link=http://reshimvse.com/mathege/?type=mc1] . Готовьтесь к ЕГЭ с нами!

7sin^2x+4sinxcosx-3cos^2x=0

Сократим на cos^2x. ОДЗ cosx≠0.

7sin^2x/cos^2x + 4sinxcosx/cos^2x - 3cos^2x/cos^2x=0

7tg^2x + 4tgx - 3 = 0

Замена tgx = t.

7t^2 + 4t - 3 = 0

D = 4^2 - 4*7*(-3) = 16 + 84 = 100

t1 = (-4 + sqrt(100))/2*7 = (-4+10)/14 = 6/14 = 3/7

t2 = (-4 - sqrt(100))/2*7 = (-4-10)/14 = -14/14 = -1

tgx = 3/7

x = arctg(3/7) + Pin, n ∈ Z

tgx = -1

x = -Pi/4 + Pin, n ∈ Z


[b]Отбор корней на окружности.[/b]


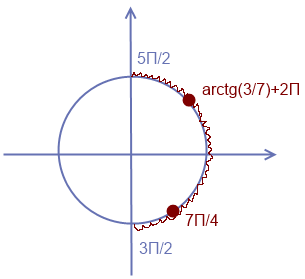
Ответ: а) -Pi/4+Pin; artctg(3/7)+Pin; б) arctg(3/7)+2Pi; 7Pi/4