Задача 13981 Все на картинке...
Условие
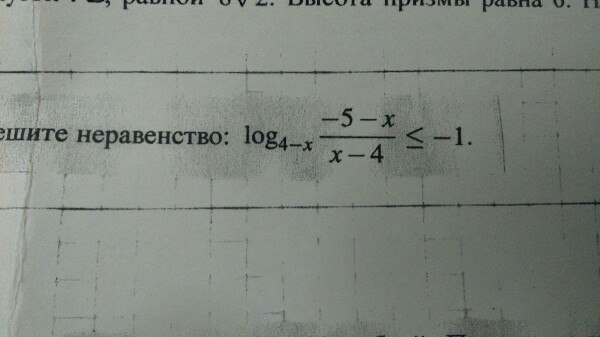
математика 10-11 класс
1044
Решение
★
-1=log_(4-x)(4-x)^(-1)
-1=log_(4-x)(1/4-x))
log_(4-x)(-5-x)/(x-4) меньше или равно log_(4-x)1/(4-x);
log_(4-x)(5+x)/(4-x) меньше или равно log_(4-x)1/(4-x).
Применяем метод рационализации логарифмических неравенств ( см. таблицу, пункт 5)
(4-x-1)*(((5+х)/(4-x))-(1/(4-x))) меньше или равно 0;
C учетом ОДЗ получаем систему неравенств:
{(5+x)/(4-x) > 0; ⇒ -5 < x < 4
{4-x > 0; 4-x ≠1 ⇒ x < 4; x≠3
{(4-x-1)*((5+х-1)/(4-x)) меньше или равно 0;⇒ x≤-4; 3≤x < 4
О т в е т. (-5; -4]U[3;4)
