Задача 13858 Решите неравенство:...
Условие
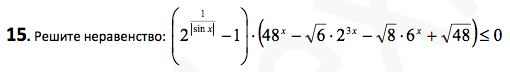
Решение
sinx≠0
x≠πk, k∈Z.
Произведение отрицательно когда множители имеют разные знаки.
Получаем совокупность двух систем
1)
{2^(1/|sinx|)-1 больше или равно 0;
{6^(x)*8^(x)-sqrt(6)8^(x)-sqrt(8)*6^(x)+sqrt(6)*sqrt(8) меньше или равно 0.
2){2^(1/|sinx|)-1 меньше или равно 0;
{6^(x)*8^(x)-sqrt(6)8^(x)-sqrt(8)*6^(x)+sqrt(6)*sqrt(8) больше или равно 0.
1)
{2^(1/|sinx|) больше или равно 2^(0);
{(6^(x)-sqrt(6))*(8^(x)-sqrt(8)) меньше или равно 0.
2){2^(1/|sinx|)-1 меньше или равно 2^(0);
{(6^(x)-sqrt(6))*(8^(x)-sqrt(8)) больше или равно 0.
1)
{1/|sinx| больше или равно 0;
{(6^(x)-sqrt(6))*(8^(x)-sqrt(8)) меньше или равно 0.
2){1/|sinx| меньше или равно 0- не имеет решений
{(6^(x)-sqrt(6))*(8^(x)-sqrt(8)) больше или равно 0.
{|sinx| > 0 - верно при всех x из ОДЗ;
{(6^(x)-sqrt(6))*(8^(x)-sqrt(8)) меньше или равно 0⇒х=1/2
О т в е т. х=1/2