Задача 13815 Помогите решить пожалуйста!...
Условие
математика
923
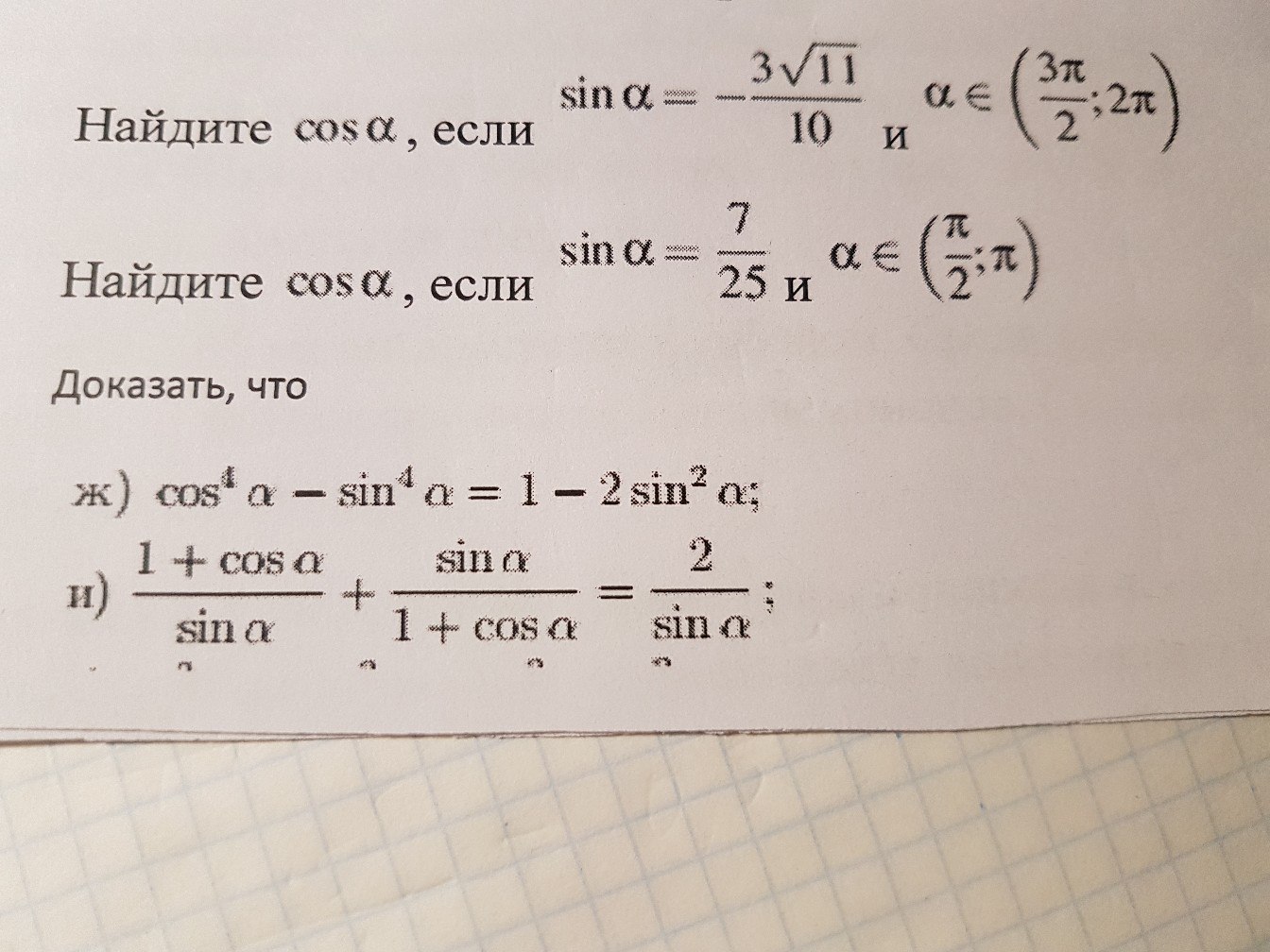
Решение
★
1)cosα=+sqrt(1-sin^2α), знак +, так как угол α в IY четверти, косинус имеет знак +.
cosα=+sqrt(1-sin^2α)=sqrt(1-(-3sqrt(11)/10)^2)=
=sqrt(1-(99/100))=sqrt(1/100)=1/10.
2)cosα=-sqrt(1-sin^2α), знак , так как угол α во II четверти, косинус имеет знак -.
cosα=-sqrt(1-sin^2α)=-sqrt(1-(7/25)^2)=
=-sqrt(1-(49/625))=-sqrt(576/625)=-24/25.
ж)cos^4α-sin^4α=(cos^2α-sin^2α)*(cos^2α+sin^2α)=
=(cos^2α-sin^2α)*1=(cos^2α-sin^2α)=
=1-sin^2α-sin^2α=1-2sin^2α
и)((1+cosα)*(1+cosα)+sinα*sinα)/(sinα*(1+cosα))=
=(1+2cosα+cos^2α+sin^2α)/(sinα*(1+cosα))=
=(2+2cosα)/(sinα*(1+cosα))=2/sinα