Задача 13785 ...
Условие
[m]
arctg(x) = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + ... + (-1)^n \frac{x^{2n+1}}{2n+1} + ...
[/m]
и соотношением [m]\pi = 4 - arctg(1) [/m]
Сравните результат со значением, полученным с помощью соответствующей встроенной функции.
Решение
arctg1=1-(1/3)+(1/5)-(1/7) + ... ? ( на каком слагаемом остановиться?), чтобы сумма была вычислена с заданной точностью.
Ряд знакочередующийся, значит остаток ряда не превышает модуля первого члена остатка.
r_(n) меньше или равно |a_(n+1)|
Найдем при каких n
|a_(n+1)| меньше 0,00001
1/(2n+1) < 1/100000 ⇒ 2n+1 > 100 000
2n > 99 999
n > 50 000
Значит, надо взять слагаемых 50 000. Это означает, что ряд сходится медленно.
И не пригоден для вычисления arctg1=π/4
Существуют приемы, которые "убыстряют" сходимость.
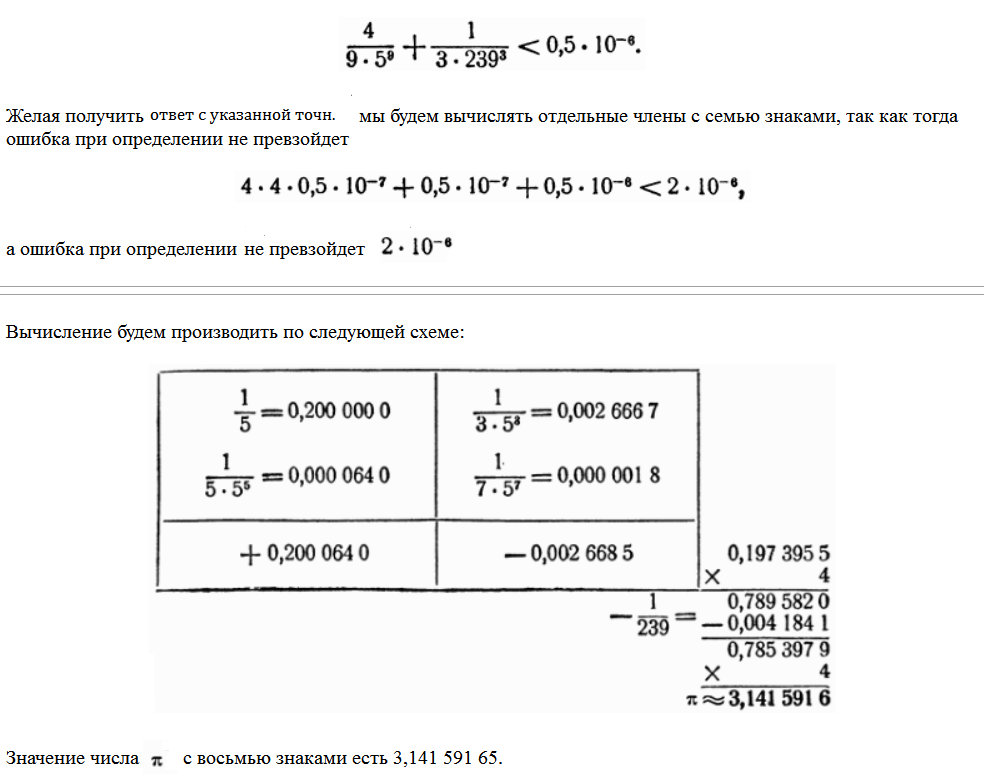
Например,