Задача 13616 Окружности радиусов 2 и 4 касаются в...

Julia_Trusova

2 октября 2017 г. в 00:00

Окружности радиусов 2 и 4 касаются в точке В. Через точку В проведена прямая, пересекающая второй раз меньшую окружность в точке А, а большую в точке С.
а) Докажите, что ВС=2АВ.
б) Найдите ВС, если АС=3√2.

Окружности могут касаться внешним и внутренним образом, поэтому в данной задаче рассмотрим 2 случая:

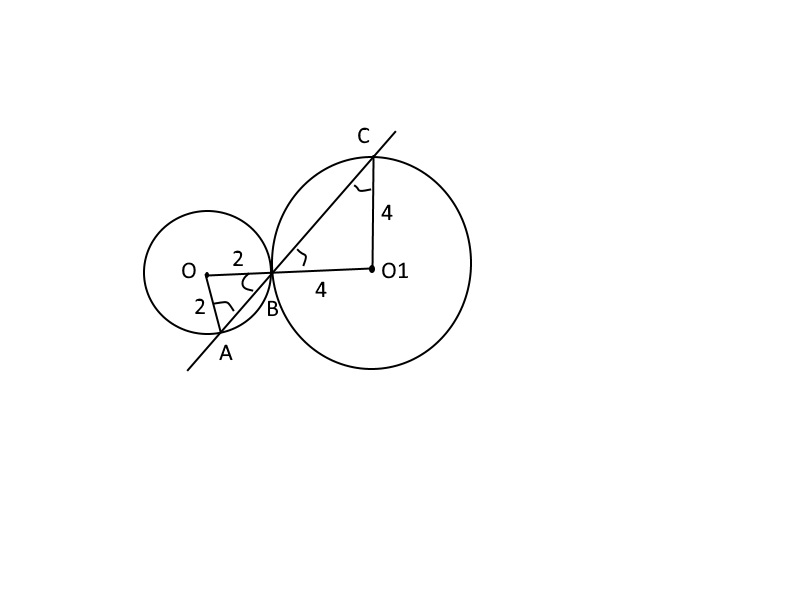
Первый случай: пусть окружности касаются внешним образом.

а)Треугольник АОВ – равнобедренный(АО и ВО – радиусы), = > угол ОАВ равен углу ОВА.
Треугольник ВО1С – равнобедренный(ВО1 и СО1 – радиусы), = > угол СВО1 равен углу ВСО1.
При этом угол ОВА равен углу О1ВС, как вертикальные.
= > угол ОАВ = углу ОВА = углу СВО1 = углу ВСО1
Значит, треугольник АОВ подобен треугольнику СО1В по трём углам,
Тогда ОВ/О1В=АВ/ВС=2/4=1/2
Откуда, ВС=2АВ

б) Из подобия треугольников следует, что ВС=2/3АС
Если АС=3√2, то ВС=2/3·3√2=2√2

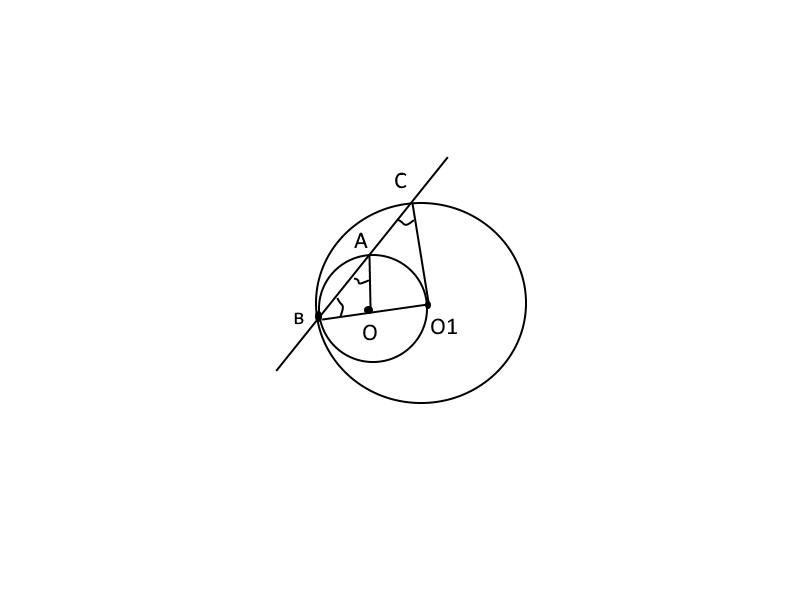
Второй случай: окружности касаются внутренним образом.

а)Треугольник АОВ – равнобедренный(АО и ВО – радиусы), = > угол ОАВ равен углу ОВА.
Треугольник СО1В – равнобедренный(СО1 и ВО1 – радиусы), = > угол О1СВ равен углу О1ВС.
= > угол ОАВ = углу ОВА = углу ВСО1
Значит, треугольник АОВ подобен треугольнику СО1В по трём углам,
Тогда ОВ/О1В=АВ/ВС=2/4=1/2
Откуда, ВС=2АВ

б)Из подобия треугольников следует, что ВС=2АС
Если АС=3√2, то ВС=2·3√2=6√2

Тогда в треугольнике СО1В: ВС > (СО1+ВО1), 6√2 > 8, что невозможно. Значит, второй случай при заданных условиях невозможен.


Ответ: б)2sqrt(2)