Задача 13543 №1. a) Решите уравнение [m]\cos 2x -...

vk97587900

2 июля 2017 г. в 00:00

№1.
a) Решите уравнение [m]\cos 2x - \sqrt{2} \sin \left( \frac{\pi}{4} - x \right) + 1 = 0[/m].

б) Укажите корни этого уравнения, принадлежащие отрезку [m]\left[ -4 \pi; -\frac{5 \pi}{2} \right][/m].

№2.
a) Решите уравнение [m]\cos 2x - \sqrt{2 \cos \left( \frac{3 \pi}{2} + x \right) - 1} = 0[/m].

б) Укажите корни этого уравнения, принадлежащие отрезку [m]\left[ \frac{3 \pi}{2}; 3 \pi \right][/m].

№3.
a) Решите уравнение [m]2 \cos \left( \frac{3 \pi}{2} + x \right) - \sin 2x = 0[/m].

б) Укажите корни этого уравнения, принадлежащие отрезку [m]\left[ -3 \pi; -\frac{3 \pi}{2} \right][/m].

№4.
a) Решите уравнение [m]\cos 2x = 1 - \cos \left( \frac{\pi}{2} - x \right)[/m].

б) Найдите все корни этого уравнения, принадлежащие промежутку [m]\left[ -\frac{5 \pi}{2}; -\pi \right][/m].

№5.
a) Решите уравнение [m]3 \cos 2x - 5 \sin x + 1 = 0[/m].

б) Укажите корни этого уравнения, принадлежащие отрезку [m]\left[ \pi; \frac{5 \pi}{2} \right][/m].

№6.
a) Решите уравнение [m]2 \cos 2x + 4 \sqrt{3} \cos 1 = 7 = 0[/m].

б) Укажите корни этого уравнения, принадлежащие отрезку [m]\left[ \frac{3 \pi}{2}; 4 \pi \right][/m].

№7.
a) Решите уравнение [m]2 \cos 2x + \sqrt{2} \sin x + 1 = 0[/m].

б) Укажите корни этого уравнения, принадлежащие отрезку [m]\left[ \frac{3 \pi}{2}; 3 \pi \right][/m].

№8.
a) Решите уравнение [m]\cos 2x - \sqrt{2 \cos x} - 5 = 0[/m].

б) Укажите корни этого уравнения, принадлежащие отрезку [m]\left[ -3 \pi; - \frac{3 \pi}{2} \right][/m].

№9.

SOVA

2 июля 2017 г. в 00:00

★

1)
По формулам приведения:
sin(π/2 – x)= cosx.
Так как
cos2x = 2cos²x–1, уравнение принимает вид
2cos²x–√2cosx=0
cosx·(2cosx–√2)=0
cosx=0 или 2cosx–√2=0.

cosx=0
x=(π/2)+πk, k∈ Z.
или
cos x =√2/2;
x = ± arccos(√2/2)+2πn, n∈ Z;
х=± (π/4)+2πn, n∈ Z.
О т в е т. а) (π/2)+πk; ± (π/4)+2πn, k, n∈ Z.
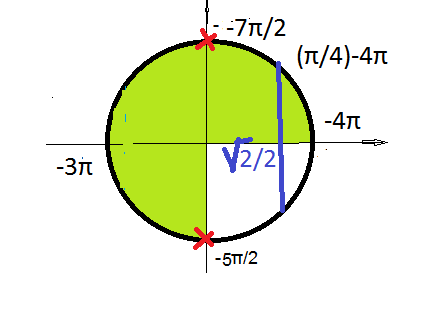
б) Указанному промежутку принадлежат корни:
(π/4)–4π=–15π/4;(–7π/2); (–5π/2) см. рисунок

3) По формулам приведения:
сos(3π/2 + x)=sinx.
Так как
sin2x =2sinxcosx, уравнение принимает вид
2•sin²x–2sinxcosx=0
2sinx·(sinx–cosx)=0
sinx=0 или sinx–cos x =0

sinx=0 ⇒ x=πk, k∈ Z;
или
sinx=cosx ⇒ tgx=1
x = arctg1+πn, n∈ Z;
х=(π/4)+πn, n∈ Z.

О т в е т.
а)πk, (π/4)+πn, k, n∈ Z.
б) Указанному промежутку принадлежат корни
–3π; (π/4)–3π=–11π/4