Задача 13502 Пусть 67-36cos^2x+60sinx /...
Условие
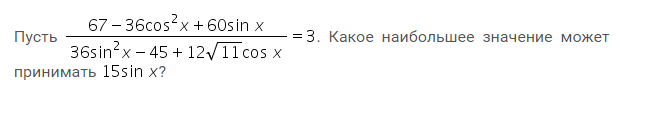
математика 10-11 класс
1650
Решение
★
cos^2x=1-sin^2x, а sin^2x=1-cos^2x,
перепишем равенство в виде
(36sin^2x+60sinx+31)/(-36cos^2x+12sqrt(11)cosx-9)=3
Замена переменной
u=sinx
v=cosx
Тогда
{(36u^2+60u+31)/(-36v^2+12sqrt(11)v-9)=3
{u^2+v^2=1
Выделяем полные квадраты
(6u+5)^2+6)/(2-(6v-sqrt(11))^2)=-3
или
(6u+5)^2+6)/(3(6v-sqrt(11))^2-6)=1

