Задача 13455 ...

slava191

04.02.2017

Окружность касается прямых АВ и ВС соответственно в точках D и Е. Точка А лежит между В и D, а тока С – между В и Е. Точки А, D, Е, С лежат на одной окружности.

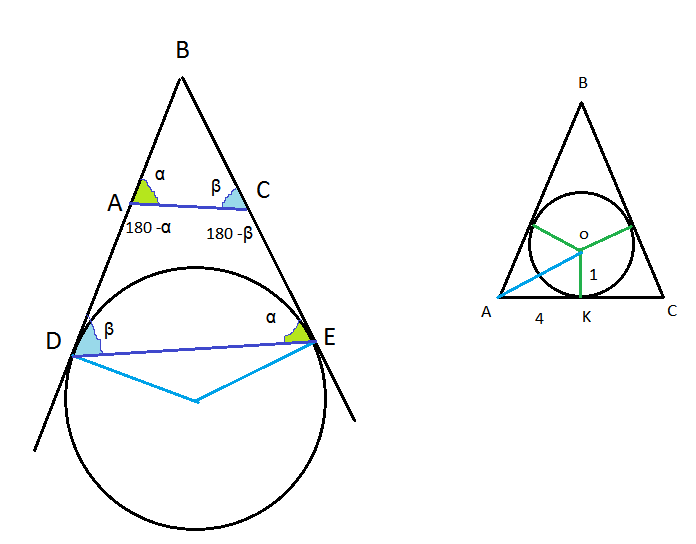
a) Доказать, что треугольники АВС и DВЕ подобны.
б) Найти площадь ABC, если АС = 8 и радиус окружности, вписанной в треугольник ABC, равен 1.

SOVA

04.02.2017

★

а) Пусть ∠ВАС=α; ∠ВСА=β.
Тогда смежные углы ∠DАС=180°-α; ∠EСА=180°-β.
Так как по условию Точки А, D, Е, С лежат на одной окружности, т.е четырехугольник АDЕС вписан в окружность, то суммы противолежащих углов равны 180°.
∠DАС+∠СED=180°;
∠АСE+∠ADE=180°.
Значит
∠СED=α; ∠АDE=β.
Треугольники АВС и DBE подобны по двум углам.
б)
По свойству касательных к окружности проведенных из одной точки- отрезки касательных равны.
BD=BE
Треугольник DBE - равнобедренный и ∠α=∠β.
Значит, треугольник АВС - равнобедренный и
АВ=ВС

Центр окружности, вписанной в треугольник АВС, - точка пересечения биссектрис.
Так как треугольник АВС - равнобедренный, центр окружности лежит на бисектрисе, высоте и медиане, проведенной из точки В.
АК=КС=4
Из прямоугольного треугольника АОК
tg∠ОАК=ОК/АО=1/4
∠ОАК=(1/2)∠BАК=α/2
Итак, в треугольнике АВС tg(α/2)=1/4
По формулам
sinα=2tg(α/2)/(1+tg^2(α/2));
сosα=(1-tg^2(α/2))/(1+tg^2(α/2));
sinα=2*(1/4)/(1+(1/4)^2)=8/17
cosα=(1-(1/4)^2)/(1+(1/4)^2)=15/17
tgα=8/15
ВК=h=4*tgα=4*(8/15)=32/15
S(Δ АВС)=АС*ВК/2=8*32/(2*15)=128/15
О т в е т. 128/15