Задача 1332 Основание пирамиды SABC – равносторонний...

slava191

29.05.2014

Основание пирамиды SABC – равносторонний треугольник со стороной 1. Вершина S проецируется в точку A, и SA = 1. Найдите угол между прямыми AB и SC.

Искомый угол это угол между прямыми CS и SD лежащими в одной плоскости, SD||AB.
SC=sqrt(2)= по т. Пифагора для треугольников SAC и DBC.
Угол S находим по т. косинусов из треугольника SDC.
CD^2=SD^2+SC^2-2*SD*SC*cosDSC
2=1+2-2*sqrt(2)*cosDSC
1=2sqrt(2)*cosDSC
cosDSC=1/2sqrt(2)=sqrt(2)/4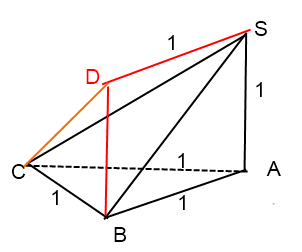

Ответ: sqrt(2)/4

Гость

30.07.2014

Ответ. arccos(1/(2sqrt2))