Задача 13213 Найдите все значения a, при каждом из...
Условие
имеет хотя бы один корень.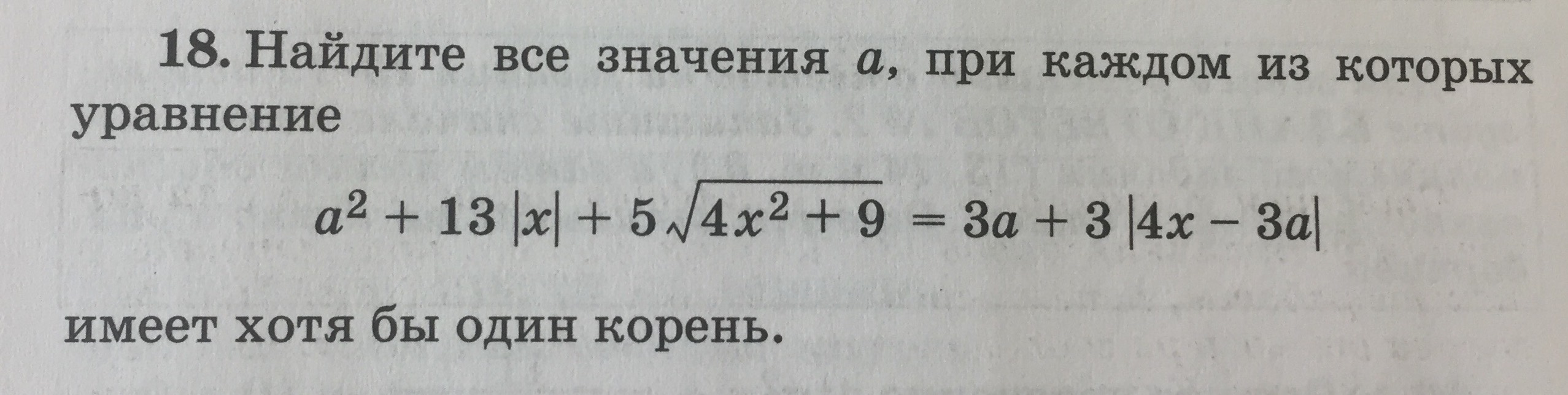
Решение
5*sqrt(4x^2+9)=3a+3*|4x-3a|-a^2-13|x|
Выражение слева принимает наименьшее значение 15 при х=0
Исследуем выражение справа.
Обозначим
g(x)=3*|4x-3a|-13|x|+3a-a^2
При х больше или равно 0
g(x)=3*|4x-3a|-13x+3a-a^2
и как бы ни раскрывался знак модуля |4x-3a| получится линейная функция с отрицательным коэффициентом при х ( либо -1, либо -25).
Функция убывает на [0;+бесконечность) и принимает наибольшее значение при х=0
Это значение равно
g(0)=3*|-3a|+3a-a^2
При x < 0
g(x)=3*|4x-3a|+13x+3a-a^2
и как бы ни раскрывался знак модуля |4x-3a| получится линейная функция с положительным коэффициентом при х ( либо 1, либо 25).
Функция возрастает на (-бесконечность;0) и принимает наибольшее значение при х=0
Итак, левая часть уравнения принимает наименьшее значение при х=0, правая часть уравнения принимает наибольшее значение при х=0.
Уравнение будет иметь решения, если g(0) меньше или равно 15.
3*|-3a|+3a-a^2 меньше или равно 15.
1) При а больше или равно 0 неравенство принимает вид:
12а-a^2-15 меньше или равно 0.
a^2-12a+15 больше или равно 0
D=144-60=84
a1=(12-2sqrt(21))/2=6-sqrt(21)
a2=6+sqrt(21).
О т в е т.(6-sqrt(21); 6+sqrt(21))
2)При а < 0 неравенство принимает вид:
-6а-a^2-15 меньше или равно 0.
a^2+6a+15 больше или равно 0
D=36-60 < 0
Неравенство выполняется при любом а ∈(- ∞;0)
О т в е т.(- ∞;0)U( 6+sqrt(21);+бесконечность)