Задача 13202 a) cos2x=sin(x+Pi/2) б) Найдите корни...
Условие
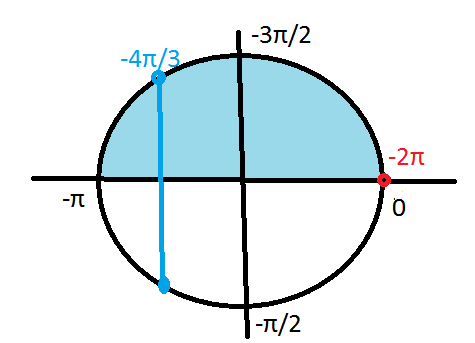
б) Найдите корни этого уравнения, принадлежащего промежутку [-2pi; -pi]
Промежутки найти по окружности
математика 10-11 класс
101017
Решение
★
sin(x+(π/2))=cosx
По формуле косинуса двойного угла
cos2x=2cos^2x-1
Уравнение принимает вид
2cos^2x-cosx-1=0
Квадратное уравнение
D=1+8=9
cosx=-1/2 или cosx=1
x=± (2π/3)+2πk, k∈Z или x=2πn, n∈Z
а) О т в е т. ± (2π/3)+2πk, k∈Z или x=2πn, n∈Z.
б) -4π/3; -2π - корни, принадлежащие указанному промежутку.