Задача 13185 Найдите все значения параметра а, при...
Условие
y = (sqrt(a+1)-2cos3x+1)/(sin^23x+a+2sqrt(a+1)+2)
содержит отрезок [2; 3]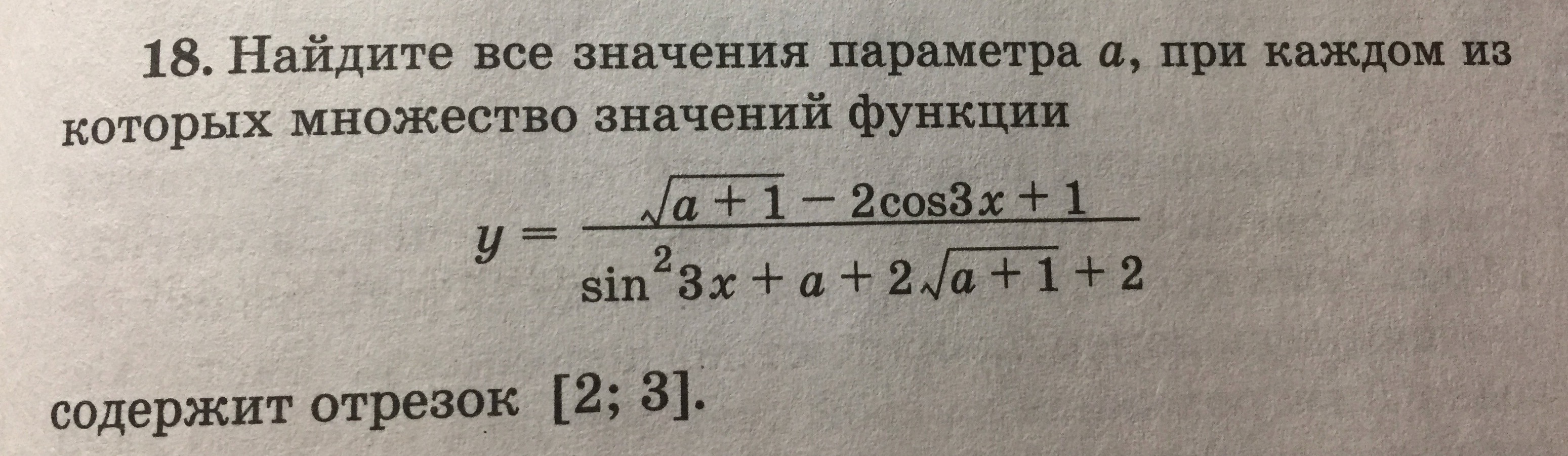
Решение
sqrt(a+1)+1=k
Тогда
y(t)=(k-2t)/(k^2+1-t^2)
Исследуем функцию на монотонность.
y`(t)=(-2*(k^2+1-t^2)-(-2t)*(k-2t))/(k^2+1-t^2)^2 < 0
Функция монотонно убывает на [-1;1]
и принимает наибольшее значение при t=-1, наименьшее при t=1.
Полагаем наибольшее значение больше или равно 3, а наименьшее значение меньше или равно 2. Тогда множество значение функции будет содержать отрезок [2;3].
Система неравенств:
{(k+2)/(k^2+1-1) больше или равно 3;
{(b-2)/(k^2+1-1) меньше или равно 2
Обратная замена
{(sqrt(a+1)+3)/(a+2sqrt(a+1)+2) больше или равно 3;
{(sqrt(a+1)-1)/(a+2sqrt(a+1)+2) меньше или равно 2
{-3a-3 больше или равно 5 sqrt(a+1);
{-2a-5 меньше или равно 3sqrt(a+1).
{9a^2-7a+16 больше или равно 0;
{-3a-3 больше или равно 0
{-2a-5 больше или равно 0
{4a^2+4a+9 меньше или равно 0
Так как последнее неравенство не выполняется ни при каких х, то похоже, что нет таких а.
Все решения
1) а=-1:
Т. к. sin^2(3x)=1-cos^2(3x) значит
у= 1-2cos3x/2-cos^2(3x)
Сделаем замену cos3x=t:
у=1-2t/2-t^2
Т. к. множество значений содержит отрезок [2;3], значит у=2 или у=3. Подставляем:
2=1-2t/2-t^2
D=28
t1=1,8... не подходит по определению косинуса сos3x от -1 до 1
t2=-0,8.. подходит
3=1-2t/2-t^2
D=64
t1=1,...не подходит
t2=-1 подходит
2) а > -1 например а=0:
у=2-2cos3x/5-cos^2(3x)
cos3x=t
y=2-2t/5-t^2
2=2-2t/5-t^2
D= 68
t1=2,...не подходит
t2= 1,...не подходит
3=2-2t/5-t^2
D=160
t1=2,...не подходит
t2=1,...не подходит
Значит, при а=-1 отрезок [2;3] удовлетворяет функции
При а > -1 отрезок не удовлетворяет функции.
Ответ: а=-1