Задача 13090 Решите неравенство:...
Условие
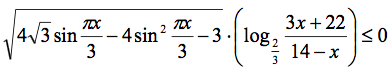
Решение
{4sqrt(3)sin(πx/3)-4sin^2(πx/3) -3больше или равно 0;
{(3x+22)/(14-x) > 0
Решаем первое неравенство
4sqrt(3)sin(πx/3)-4sin^2(πx/3)-3 больше или равно 0;
или
4sin^2(πx/3)-4sqrt(3)sin(πx/3)+3меньше или равно 0;
замена переменной
sin(πx/3)=t;
4t^2-4sqrt(3)+3меньше или равно 0;
D=(-4sqrt(3))^2-4*4*3=0
Значит неравенство можно записать в виде:
(2t-sqrt(3))^2 меньше или равно 0
Оно верно лишь при t=sqrt(3)/2
sin(πx/3)=sqrt(3)/2
(πx/3)=(π/3)+2πk, k∈Z или (πx/3)=(2π/3)+2πk, k∈Z
Сокращаем на (π)
(x/3)=(1/3)+2k, k∈Z или (x/3)=(2π/3)+2n, n∈Z
х=1+6k, k∈Z или х=2+6n, n∈Z
Решаем второе неравенство:
(3x+22)/(14-x) > 0 ⇒ (-22/3;14)
Пересечением двух множеств служат точки:
х=-5;1;7;13
и
х=-4;2;8
ОДЗ: х=-4;-5;1;2;7;8;13
В условиях ОДЗ неравенство принимает вид:
log_(2/3)(3x+22)/(14-x) меньше или равно 0;
log_(2/3)(3x+22)/(14-x) меньше или равно log_(2/3)1;
основание логарифмической функции 0 < (2/3) < 1 функция убывает, значит
(3x+22)/(14-x) больше или равно 1;
(3х+22-14+х)/(14-х) больше или равно 0
(4x+8)/(14-x)больше или равно 0
____[-2] __+___ (14) ___
х ∈ [-2;14) .
С учетом ОДЗ получаем ответ
x=1;x=2; х=7;х=8;х=13
О т в е т. 1;2; 7;8;13