Задача 1298 В правильной треугольной призме...

slava191

23.05.2014

В правильной треугольной призме ABCA1B1C1 сторона основания равна 4, высота - 10. Точки К и М -середины ребер АС и А1В1 соответственно. Найдите косинус угла между прямыми АС1 и КМ.

1)Угол между данными скрещивающимися прямыми равен углу между прямыми МK и KL лежащими в одной плоскости и KL || AC1. Это угол MKL
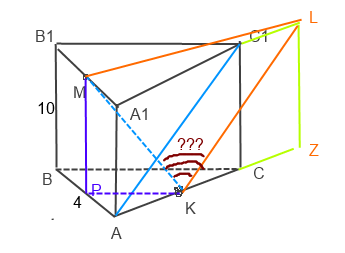
2)MP=10, KP=2 как средняя линия треугольника
MK=sqrt(100+4)=2sqrt(26) по т. Пифагора из MKP
KL=AC1=sqrt(100+16)=2sqrt(29) по т. Пифагора из AC1C
ML находим по теореме косинусов из треугольника MA1L
ML^2=A1M^2+A1L^2-2*A1M*A1L*cos60
ML=sqrt(4+36-2*2*6*cos60)=sqrt(28)=2sqrt(7)
Теперь находим нужный нам угол MKL по теореме косинусов.
ML^2=KL^2+MK^2-2*MK*KL*cosMKL
28=116+104-8sqrt(754)*cosMKL
24=sqrt(754)*cosMKL
cosMKL=24/sqrt(754)=24sqrt(754)/754=12sqrt(754)/377


Ответ: arccos(12sqrt(754)/377)