Задача 1295 В основании прямой призмы ABCDA1B1C1D1...

slava191

23.05.2014

В основании прямой призмы ABCDA1B1C1D1 лежит ромб ABCD с диагоналями AC=6 и BD=12. Высота призмы равна sqrt(15). Найдите угол между прямыми AB1 и D1C.

угол между скрещивающимися прямыми AB1 и D1C будет равен величине угла между прямыми AB1 и BA1.
AB=sqrt(36+9)=sqrt(45)
tgAB1B=sqrt(45)/sqrt(15)=sqrt(3)
Значит угол AB1B=60 градусов
Так как треугольник B1BA прямоугольный
угол BAB1=90-60=30=CBA, значит угол между BC и CA=180-30-30=120
В таком случаем угол между прямыми AB1 и BA1 будет равен 180-120=60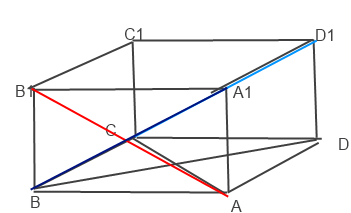

Ответ: 60