Задача 12897 ...

slava191

14.01.2017

На стороне АВ треугольника АВС отмечена точка М, отличная от вершин, что МС=АС. Точка Р симметрична точке А относительно прямой ВС.

А) Докажите, что около четырехугольника ВМСР можно описать окружность.
Б) Найдите длину отрезка МР, если известно, что АВ=6, ВС=5, СА=3

SOVA

15.01.2017

★

А) См. рис. 1
Треугольник АМС - равнобедренный, АС=МС=3.
Значит, ∠МАС=∠АМС.
Пусть ∠МАС=∠АМС=α
Тогда ∠ВМС=180 градусов -α.
По построению AP⊥BC и АК=КР.
Из равенства прямоугольных треугольников АВК и ВРК, следует, что АВ=ВР и ∠ВАР=∠ВРА.
Из равенства прямоугольных треугольников АКС и ВКС, следует, что АС=СР и ∠РАС=∠АРС.
Значит, ∠ВАС=∠ВАР+∠РАС=∠ВРА+∠РСА=∠ВРС.
∠ВАС=α ⇒∠ВРС=α

∠ВМС+∠ВРС=(180 градусов -α)+α=180 градусов.

Сумма противоположных углов четырехугольника ВМСР равна 180 градусов, около четырехугольника можно описать окружность.

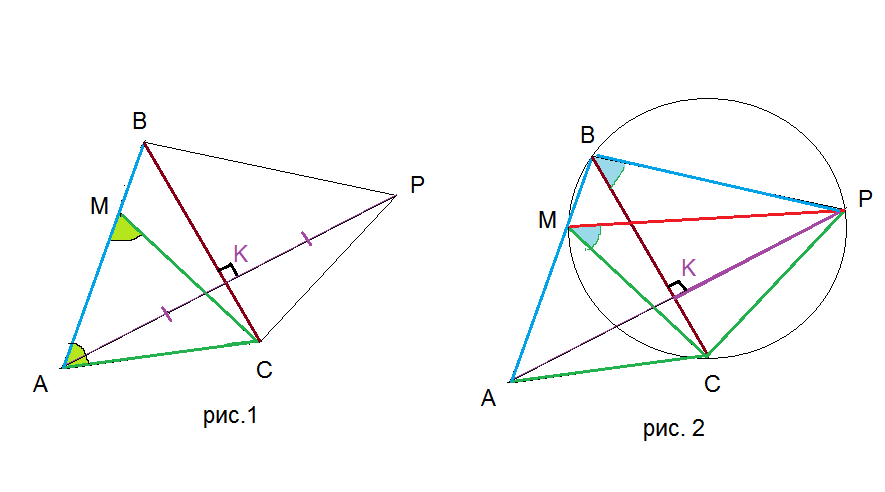
Б)См. рис. 2
∠РВС=∠ВМС как углы опирающиеся на одну и ту же дугу РС.
Найдем cos ∠РВС по теореме косинусов из треугольника ВРС:
ВР=АВ=6; РС=АС=3; ВС=5.

РС^2=BC^2+BP^2-2*BC*BP*cos ∠РВС ⇒
cos ∠РВС =(5^2+6^2-3^2)/(2*5*6)=13/15.
Из треугольника МРС по теореме косинусов:
РС^2=MC^2+MP^2-2*MC*MP*cos ∠РMС
cos ∠РMС=cos ∠РВС=13/15.
3^2=3^2+MP^2-2*3*MP*(13/15)
MP^2-(26MP/5)=0
MP=26/5=5,2.
О т в е т. Б) МР=5,2.