Задача 12853 1/cos^2 + 1/sin(x-Pi/2) = 2; [-2Pi;...
Условие
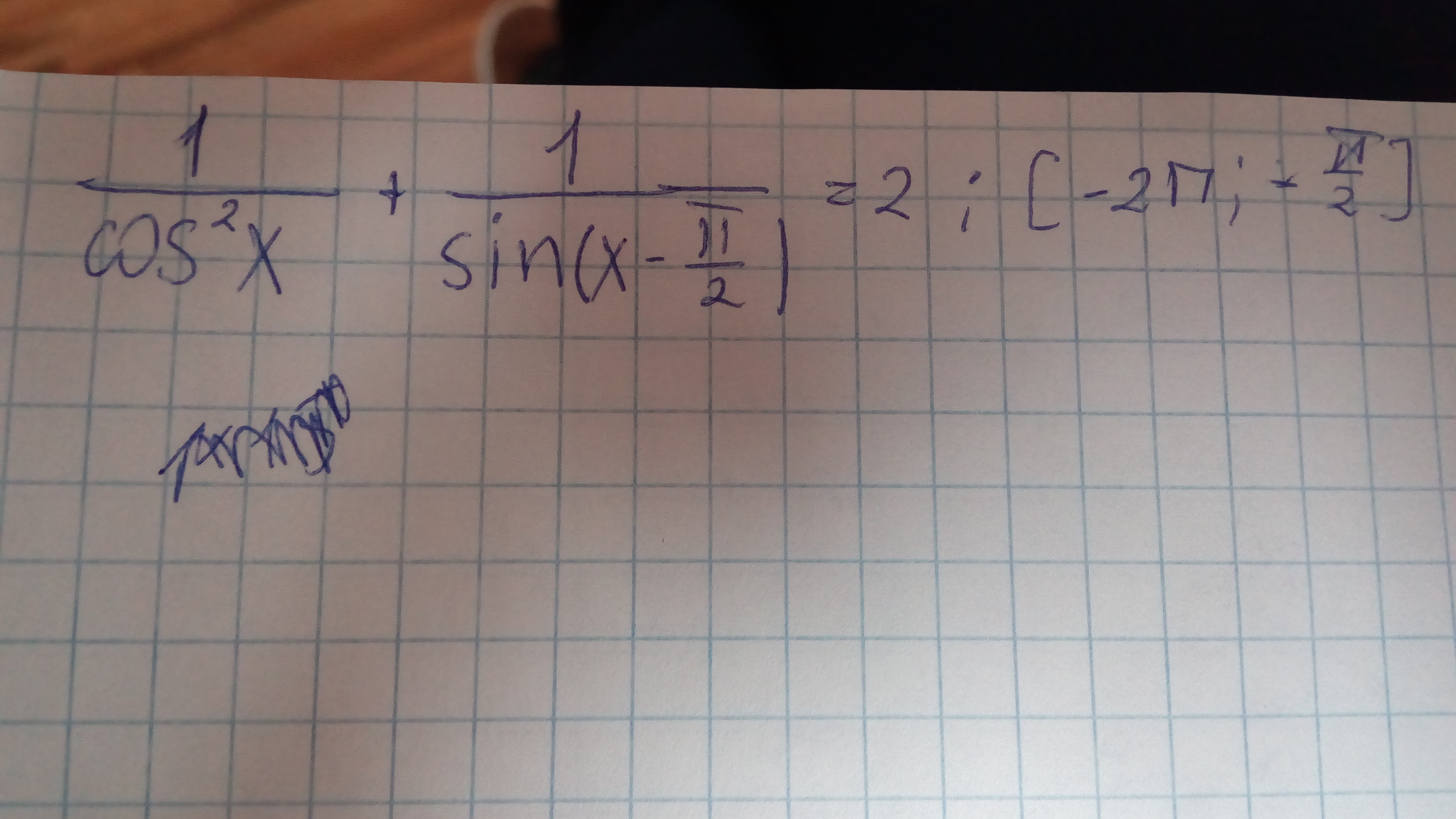
математика 10-11 класс
12864
Решение
★
sin((π/2)-x)=cosx.
sin(x-(π/2))=-cosx
Уравнение принимает вид
(1/cos^2x)-(1/cosx)=2
или
(2cos^2x+cosx-1)/cos^2x=0
{2cos^2x+cosx-1=0;
{cosx≠0
Замена переменной
cosx=t
2t^2+t-1=0
D=1+8=9
t=-1 или t=1/2
cosx=-1 ⇒x=π+2πn, n∈Z
или
cosx=1/2 ⇒±(π/3)+2πk, k∈Z
Б)х=-2π; х=-4π/3; х=-2π/3 - корни уравнения, принадлежащие отрезку [-2π; -π/2].
О т в е т.
А)±(π/3)+2πk, π+2πn, k, n∈Z
Б) -π; -π/3; (π/3)-2π=-5π/3