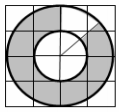
Задача 12839 Площадь закрашенной фигуры равна...

slava191

11.01.2017

Площадь закрашенной фигуры равна (525/8)*Pi. Найдите радиус большого круга.

Пусть R - радиус большей окружности, а r - радиус меньшей. Закрашенная часть составляет 7/8 площади, которую мы получим если из площади всей окружности (PiR^2) вычтем внутреннюю окружность (Pir^2) и эта площадь равна (525/8)*Pi по условию задачи. Тогда можно составить уравнение.

[b](7/8)(PiR^2 - Pir^2) = (525/8)*Pi[/b]

По рисунку видно, что радиус внутренней окружности составляет половину от радиуса всей окружности, тогда [b]r = (1/2)R[/b].

Теперь наше уравнение примет вид

[b](7/8)(PiR^2 - Pi((1/2)R)^2) = (525/8)*Pi[/b]

Сразу видно, что Pi можно сократить

(7/8)(R^2 - ((1/2)R)^2) = 525/8

Также сразу можно домножить все на 8.

7(R^2 - ((1/2)R)^2) = 525

7(R^2 - (1/4)R^2) = 525

7((4R^2 - R^2)/4) = 525

7(3R^2/4) = 525

3R^2/4 = 525/7

3R^2/4 = 75

R^2 = 75*4/3 = 100

R = sqrt(100)

Мы получаем 2 корня R1 = 10 и R2 = -10. Но отрицательный корень нам не подходит. Так как не может быть отрицательный радиус. Значит в ответ пишем 10.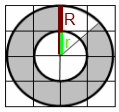

Ответ: 10