Задача 12727 (1-sqrt(1-4log^2_(8)x))/log8x < 2...
Условие
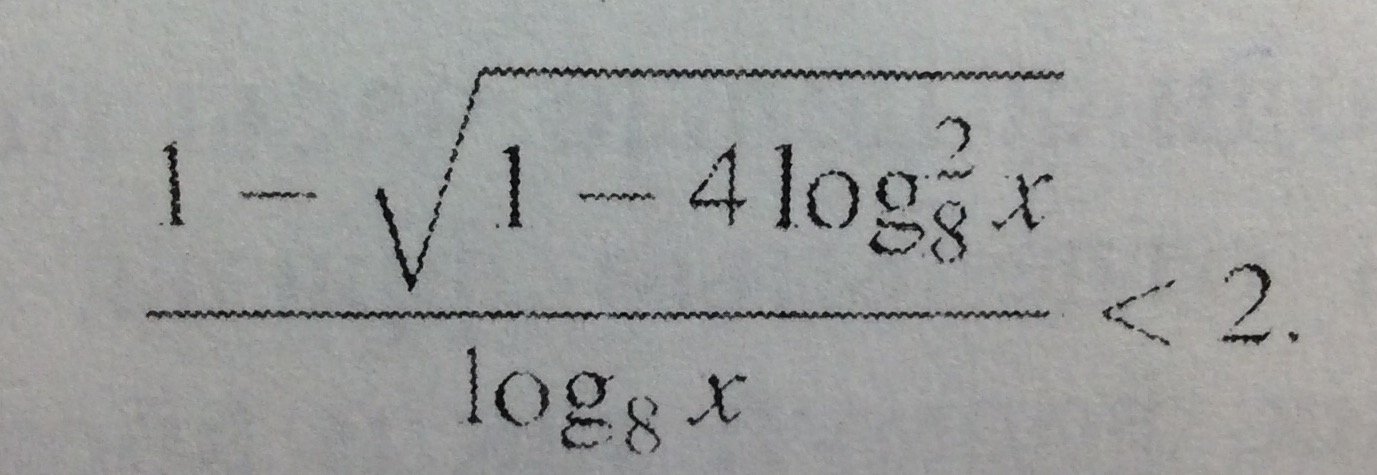
математика 10-11 класс
14726
Решение
★
{x > 0;
{log_(8)x≠ 0⇒ x ≠ 1
Замена переменной:
log_(8)x=t;
Неравенство принимает вид:
(1-sqrt(1-4t^2))/t < 2
или
1-sqrt(1-4t^2)-2t < 0;
sqrt(1-4t^2) > 1-2t;
1) {1-2t меньше или равно 0⇒ t≥1/2;
{1-4t^2 больше или равно 0⇒ -1/2 < t < 1/2
Система не имеет решений
или
2) {1-2t > 0 ⇒ t < 1/2;
{1-4t^2 > (1-2t)^2 ⇒ 4t(2t-1) < 0 ⇒ 0 < t < 1/2.
х∈(0;1/2)- удовлетворяет ОДЗ.
0 < log_(8)x < 1/2
log_(8)1 < log_(8)x < log_(8)8^(1/2)
логарифмическая функция с основанием 8 возрастает, поэтому
1 < x < 8^(1/2)
О т в е т. (1;2sqrt(2)).