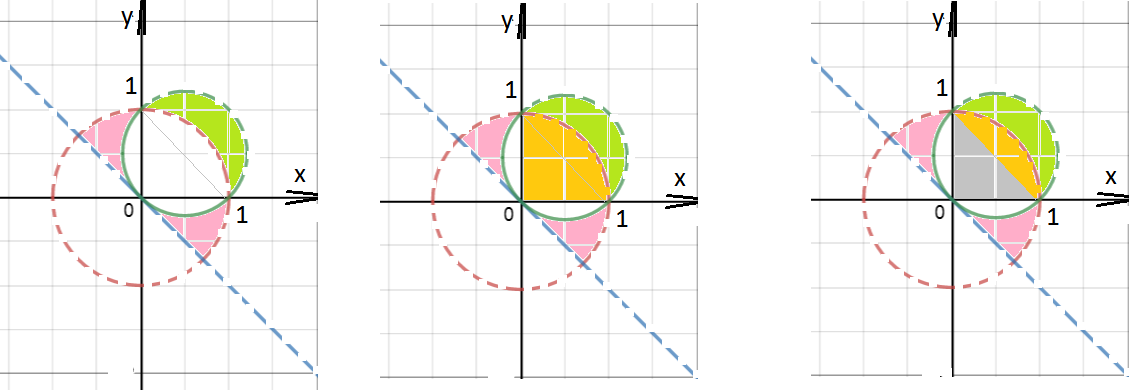Задача 12678 ...

slava191

02.01.2017

А) На координатной плоскости Оху изобразите фигуру, заданную неравенством log(x^2+y^2)(x+y) > 1

Б) Найдите площадь полученной фигуры.

SOVA

02.01.2017

★

1) ОДЗ: x+y > 0 ⇒ y > - x
Это часть плоскости, расположенная выше прямой у=-х.
x^2+y^2 > 0 при любом х
х^2+y^2≠1 - точки, лежащие на окружности с центром (0;0) и радиусом 1.
Изображаем окружность пунктирной линией.

Так как 1=log_(x^2+y^2)(x^2+y^2), то
log_(x^2+y^2)(x+y) > log_(x^2+y^2)(x^2+y^2)

Применяя метод рационализации логарифмических неравенств, получаем неравенство:
(x^2+y^2-1)*(x+y-x^2-y^2) > 0

Решаем методом интервалов.
x^2+y^2-1=0
x^2+y^2=1 - уравнение окружности с центром (0;0) и радиусом R=1.
x+y-x^2-y^2=0
(x-(1/2))^2+(y-(1/2))^2=1/2 - уравнение окружности, с центром в точке (1/2; 1/2) и радиусом r=sqrt(1/2).

А)Неравенство с учетом ОДЗ задает две области ( розового цвета и зеленого цвета) на плоскости хОу ( см. рис. 1).
Б)
Площадь этих областей находим, пользуясь формулами планиметрии нахождения площади круга, половины круга, четвертой его части и площади прямоугольного равнобедренного треугольника c катетами, равными R=1
S(желтой четверти круга)=πR^2/4=π/4
S(желтого сегмента)=S(желтой четверти круга)-S(прямоугольного треугольника)=(πR^2/4)-(R*R/2)=
=(π/4)-(1/2)=(π-2)/4.

S(розовой области )=(1/2)S(круга R=1)-(1/2)S(круга r=sqrt(1/2))-S(желтого сегмента)=
=(π/2)-(π/4)-((π-2)/4).

S(зеленой области)=(1/2)S(круга r=sqrt(1/2))-S(желтого сегмента)=(π/4)-((π-2)/4).

S=S(розовой области)+S(зеленой области)=

=(π/2)-(π/4)-((π-2)/4)+ (π/4)-((π-2)/4)=

=(π/2)-2*((π-2)/4)=(π/2)-((π-2)/2)=(π-π+2)/2=2/2=1.
Б) О т в е т. 1