Задача 12677 Решите неравенство 4^x+16/x^2 больше или...
Условие
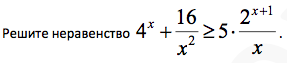
Решение
Замена переменной:
2^x=u;
4/x=v.
2^(x+1)/x=(2^x)*(2/x)=u*(v/2)=uv/2
Неравенство принимает вид:
u^2-(5/2)uv+v^2 больше или равно 0;
Делим неравенство на u^2 > 0
1-2,5(v/u)+(v/u)^2 больше или равно 0
Замена
v/u=t.
t^2-2,5t+1 больше или равно 0;
D=6,25-4=2,25
t1=(2,5-1,5)/2=0,5 или t2=(2,5+1,5)/2=2
t меньше или равно 0,5 или t больше или равно 2
(2^(2-x)/x) меньше или равно2^(-1) (2^(2-x)/x) больше или равно 2
2^(2-х)меньше или равно x/2 или 2^(2-х) больше или равно 2x
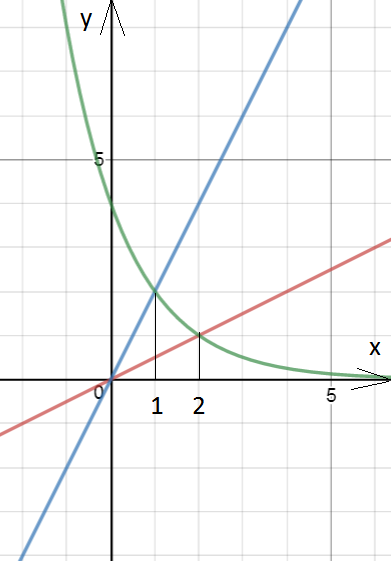
Строим графики
у=х/2;
у=2^(2-x);
y=2x
x∈[2;+ бесконечность) или x∈(- бесконечность;1]
C учетом ОДЗ получаем ответ
О т в е т.(- бесконечность;0)U(0;1]U[2;+ бесконечность).
Все решения
t ≤ 0,5 , t ≥ 2.
Окончательный ответ (0;1], [2; +∞)