Задача 12674 ...

slava191

1 февраля 2017 г. в 00:00

Найдите наименьшее значение выражения

√2+2x²–2x+√2+2x²–2x√3

SOVA

1 марта 2017 г. в 00:00

★

Обозначим у=√2+2x²–2x+√2+2x²–2√3x.
Пусть f(x)=√2+2x²–2x,
g(x)=√2+2x²–2√3x,
тогда
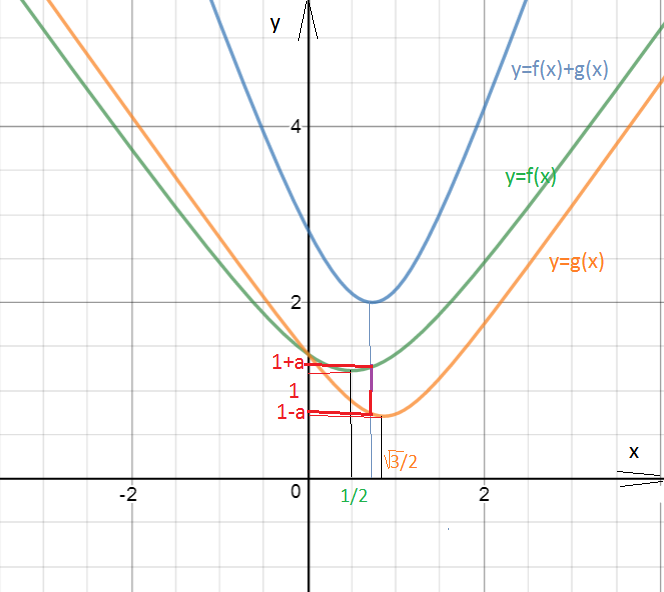
у=f(x)+g(x)
Функция у=f(x) определена при любом х:
2+2x²–2x > 0 при любом х, так как дискриминант квадратного трехчлена D=4–16 < 0
Функция у=g(x) определена при любом:
2+2x²–2√3x > 0 при любом х, так как дискриминант квадратного трехчлена D=12–16 < 0.

Функция у=f(x) принимает наименьшее значение в точке х=1/2, так как подкоренное выражение принимает наименьшее значение в точке х=1/2
(2+2x²–2x)`=4x–2
4x–2=0
x=1/2
f(1/2)=√2+2·(1/2)²–2·(1/2)=√3/2 > 1

Функция у=g(x) принимает наименьшее значение в точке х=√3/2, так как подкоренное выражение принимает наименьшее значение в точке х=√3/2
(2+2x²–2√3x)`=4x–2√3
4x–2√3=0
x=√3/2
√2+2·(√3/2)²–2·(√3/2)·√3=
=√1/2 < 1.

Сумма двух функций f(x)+g(x) принимает наименьшее значение в том случае, когда
f(x)=1+a,
g(x)=1–a
см. рисунок
у(наименьшее)=1+а+1–а=2
О т в е т. 2