Задача 12670 ...
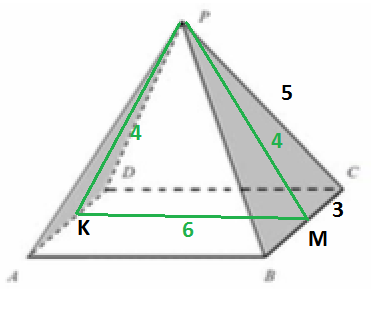
Условие
Решение
Плоскость РКМ перпендикулярна плоскостям РАD и РВС, так как РК⊥AD и КМ⊥AD, значит AD⊥пл. РКМ, пл. PAD проходит через перпендикуляр AD к плоскости РКМ.
Значит плоскости РАD И РКМ перпендикулярны.
Аналогично, РМ ⊥ВС и КМ⊥ВС, значит ВС⊥пл. РКМ, пл. PВС проходит через перпендикуляр ВС к плоскости РКМ.
Значит плоскости РВС И РКМ перпендикулярны.
РМ - высота, медиана и биссектриса равнобедренного треугольника РВС.
Из прямоугольного треугольника РМС
РМ=4 ( египетский треугольник).
По теореме косинусов из треугольника КМР:
КМ^2=KP^2+PM^2-2*KP*PM*cos∠KPM ⇒
cos∠KPM=(4^2+4^2-6^2)/2*4*4=4/32=1/8 = 0.125