Задача 12629 Дан треугольник ABC. На луче BA за...

veron01101

28 декабря 2016 г.

Дан треугольник ABC. На луче BA за точкой A взяли точку X, а на луче BC за точкой C взяли точку Y так, что XA=YC=AC. Прямые AY и CX пересекаются в точке Z. Из точки Z опустили перпендикуляр ZH на AC. Известно, что AB=8, CB=7, AH=3. Найдите CH

SOVA

1 января 2017 г. в 00:00

★

Пусть ХА=УС=АС=а.
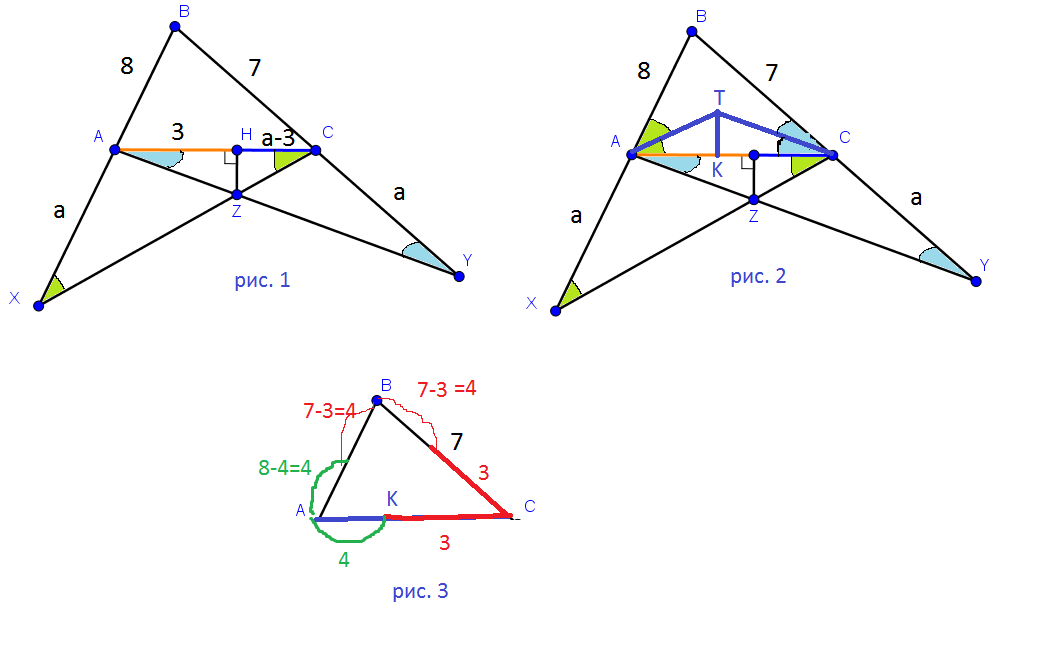
Δ ХАС – равнобедренный, ∠АХС=∠АСХ.
Обозначим ∠АХС=∠АСХ=α.
Δ АСУ – равнобедренный, ∠САУ=∠СУА.
Обозначим∠САУ=∠СУА=β.(см. рис. 1)

Так как внешний угол треугольника равен сумме внутренних с ним не смежных, в треугольнике АВС: ∠ВАС=2α, ∠ВСА=2β.
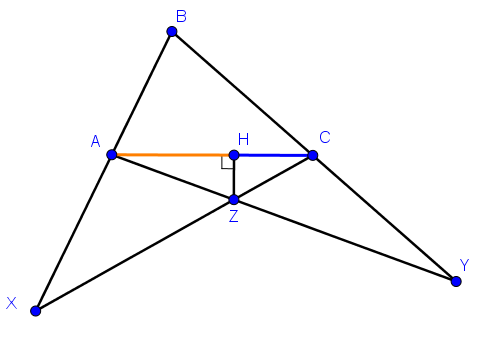
Проведем биссектрисы угла А и С треугольника АВС, они пересекаются в точке Т.
АТСZ– параллелограмм. ( см. рис.2)
AT||CX и СT || AY ( внутренние накрест лежащие углы равны).
Диагональ АС параллелограмма АТСZ делит его на два равных треугольника: ΔАTС =Δ ACZ.
Проведем TK ⊥ AC
СК=АН=3

Кроме того, так как T – центр вписанной в треугольник АВС окружности, то отрезки касательных проведенных из одной точки равны.( см. рис. 3)
Значит отрезки касательных, проведенных из точки В равны BC–2=7–3=4
Отрезки касательных проведенных от точки А тоже равны.
8–4=4
Значит АК=4
АС=АК+КС=4+3=7
СН=7–3=4
О т в е т. 4