Задача 12625 Диагонали трапеции делят ее на четыре...
Условие
Решение
Доказательство. Проводим высоты ВН=СК=h.
S(Δ ABD)=S(Δ ACD)=AD*h/2.
S(Δ ABD)-S(Δ AOD)=S(Δ ACD)-S(Δ AOD).
2) Площади треугольников, имеющих общую высоту, относятся как основания.
Треугольники АВО и ВОС имеют общую высоту.
Треугольники АОD и CОD так же имеют общую высоту.
Поэтому
S(Δ ABO):S(Δ BOC)=S(ΔAOD):S(ΔCOD)=AO:OC
Пусть
S(Δ ABO)=S(Δ СOD)=x
x:S(Δ BOC)=S(ΔAOD):x
По свойству пропорции произведение крайних членов пропорции равно произведению средних.
S(Δ BOC)*S(ΔAOD)=x^2
Равенство возможно, если S(Δ BOC)=4;S(ΔAOD)=16;
S(Δ ABO)=S(Δ СOD)=8
4*16=8^2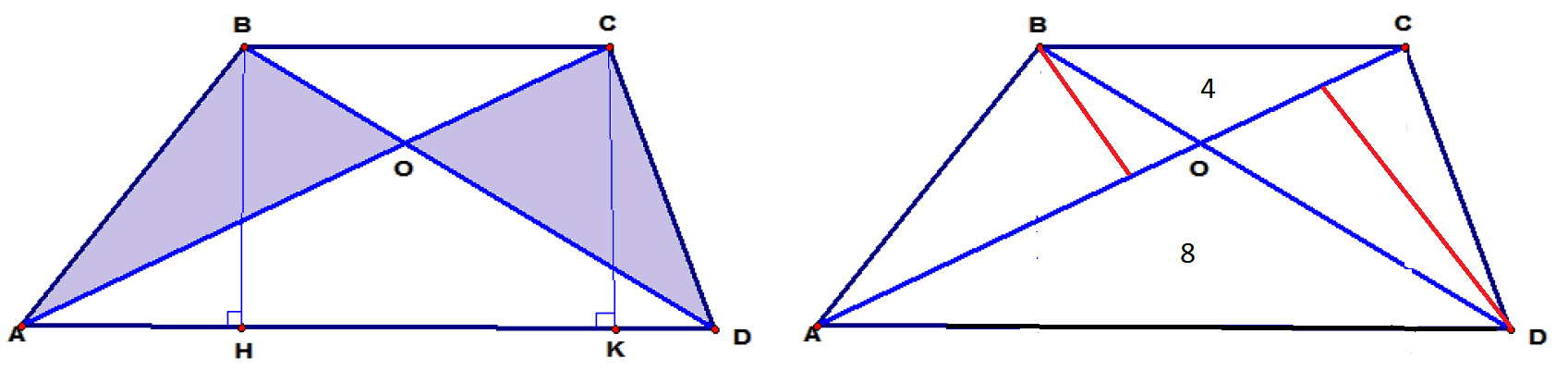
Все решения