Задача 12624 ...

veron01101

28.12.2016

В клетчатом квадрате 104×104 отмечены центры всех единичных квадратиков (всего 10816 точек). Какое наименьшее число прямых, не параллельных сторонам исходного квадрата, нужно провести, чтобы вычеркнуть все отмеченные точки?

SOVA

10.01.2017

★

Проведем все прямые, параллельные одной из диагоналей квадрата и содержащие более одной из отмеченных точек — таких прямых (зеленые прямые на рисунке).
в квадрате со стороной 4 - 5 прямых;
в квадрате со стороной 6 - 9 прямых;
в квадрате со стороной 8 - 13 прямых;
...
в квадрате со стороной 104 - 203 прямых.
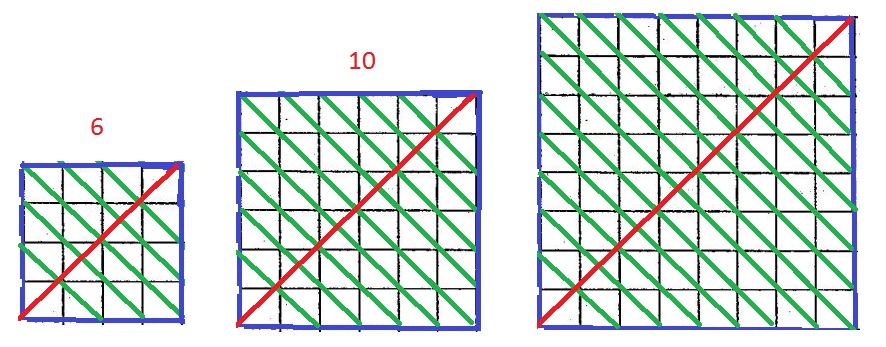
Невычеркнутыми остаются две угловые точки. Их можно вычеркнуть, проведя еще одну прямую — другую диагональ (красного цвета).
Тогда
в квадрате со стороной 4 - 6 прямых;
в квадрате со стороной 6 - 10 прямых;
в квадрате со стороной 8 - 14 прямых;
...
в квадрате со стороной 104 - 206 прямых.
Вообще, в квадрате со стороной n
2*(n-2)+2 прямых.

Докажем, что нельзя обойтись меньшим числом прямых.
Рассмотрим центры единичных квадратиков, расположенных по периметру большого квадрата. Прямая, не параллельная стороне квадрата, может вычеркнуть не более двух таких точек.
О т в е т. 206 прямых.