Задача 12620 На основании AD трапеции ABСD отмечена...

veron01101

28.12.2016

На основании AD трапеции ABСD отмечена точка F. Оказалось, что AB=BF и FC=CD. Радиусы окружностей, вписанных в треугольники ABF, FCD, BFC равны 2, 5 и 4 соответственно. Найдите отношение AF:FD

SOVA

29.12.2016

★

Пусть AB=BF=a; FС=CD=b
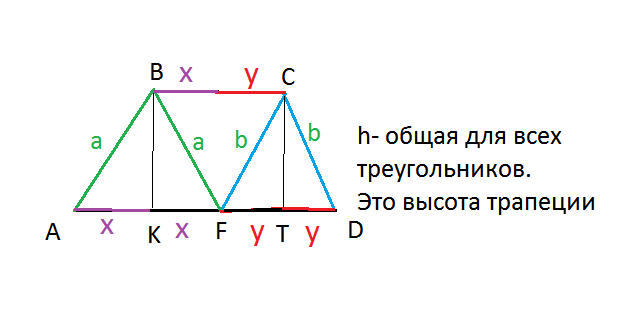
Высота трапеции h=BK=CT

Треугольник АВF – равнобедренный.
Высота СК делит сторону AF пополам
АК=КF=х
Треугольник FCD – равнобедренный.
Высота СT делит сторону FD пополам
FT=TD=y
Поэтому BC=x+y=AD/2
Запишем площади треугольников по формулам
S=r*p, S– площадь треугольника , р – полупериметр
S=a*h/2
и получим систему трех уравнений с четырьмя переменными.
{2х*h/2=2*(2x+2a)/2;
{2y*h/2=5*(2y+2b)/2;
{(x+y)*h/2=(a+b+x+y)*4/2.
или
{х*h=2x+2a;
{y*h=5y+5b;
{(x+y)*h/2=2a+2b+2x+2y.
Складываем первое и второе
{(x+y)*h=2x+5y+2a+5b;
{(x+y)*h/2=2x+2y+2a+2b.
Вычитаем из первого второе:
(x+y)*h/2=3y+3b ⇒ y+b=(x+y)*h/6
так как y*h=5y+5b, то
(х+у)*h/6=y*h/5
или
5*(x+y)=6y
5x=y
x/y=1/5
О т в е т. АF:FD=x:y=1:5.