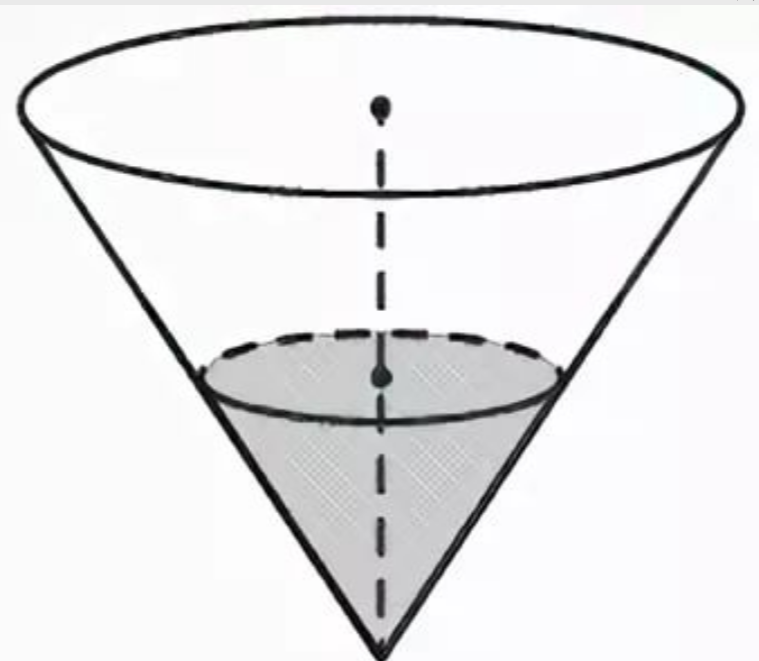
Задача 12533 В сосуде, имеющем форму конуса, уровень...

Julia_Trusova

24.12.2016

В сосуде, имеющем форму конуса, уровень жидкости достигает 1/4 высоты. Объём жидкости равен 5 мл. Сколько миллилитров жидкости нужно долить, чтобы наполнить сосуд доверху?

Vконуса=1/3Sосн.*h=1/3Pir^2*h
h1=1/4h, где h1 - уровень жидкости в сосуде, = > r1=1/4r
Тогда объём жидкости в сосуде равен V1=1/3Pi(r1)^2*h1=1/3Pi(r/4)^2*1/4*h=1/64*1/3*Pir^2*h=5
= > 1/3Pir^2*h=320 (мл) - объём сосуда
320-5=315 (мл) - столько жидкости нужно долить

Ответ: 315

vk397114329

10.08.2018

Решение:
V-объем всего конуса;
V1-объем нижнего (заполненного жидкостью равного 5 мл)
Эти конусы подобны с коэффициентом подобия к=1/4.
Отношение объемов подобных тел равно кубу коэффициента подобия, поэтому
V1/V=(1/4)^3 или 5/V=1/64.откуда V=5*64=320(мл)
Определим количество жидкости,которое дополнит сосуд доверху:
320(мл)-5(мл)=315(мл).
Ответ: 315

u9015464229

17.09.2017

Vконуса = 1/3 · h · Socн = 1/3 · h · π · r в квадрате.
D/2 = r
V = 1/3 · h · π · (D/2) в квадрате.
Для решения данной задачи будем рассматривать объемы двух конусов:
объем конуса, у которого уровень жидкости равен 1/4 высоты – Vмен,
объем конуса, наполненный доверху – Vбол.
Vбол = 1/3 · h · π · (D/2) в квадрате
Vмен = 1/3 · h/4 · π · (D/2/4) в квадрате = (1/3 · h · π · (D/2)2) / (4 · 16) = Vбол / 64 = 5 мл
Vбол = 5 · 64 = 320 мл

Осталось вычислить, сколько жидкости необходимо долить, чтобы заполнить сосуд доверху:
Vбол – Vмен = 320 - 305 = 315 мл необходимо долить.

Ответ: 315 мл