Задача 12471 Полное исследование графика:...
Условие
1) найти область определения функции; выяснить, является ли функция четной (нечётной),периодической
2) найти точки пересечения графика с осями координат и промежутки, на которых f(x) > 0 и f(x) < 0
3) найти асимптоты графика функции
4) вычислить f'(x), найти промежутки возрастания (убывания) функции и её экстремумы
5) вычислить f''(x), определить направления выпуклости и найти точки перегиба
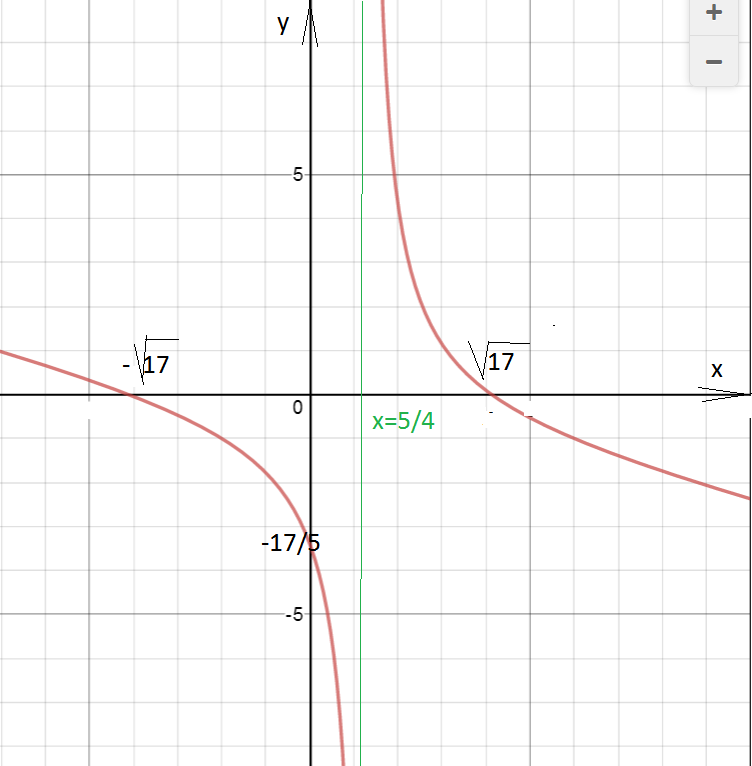
6) изобразить график функции
Решение
4х-5≠0
х≠5/4.
Функция не является ни четной, ни нечетной.
у(-х)=(17-х^2)/(-4x-5)
y(-x)≠y(x)
y(-x)≠-y(x)
Функция не является периодической.
2)Точки пересечения графика с осями координат:
с осью Ох:
у=0
17-x^2=0
x=-sqrt(17) или х=sqrt(17)
f(x) > 0 на (-∞;-sqrt(17))и (sqrt(17);+∞)
f(x) < 0 на (-sqrt(17);sqrt(17)).
3) x=5/4 -вертикальная асимптота.
lim_(x→(5/4)+0)f(x)=+∞
lim_(x→(5/4)-0)f(x)=-∞
Горизонатльных асимптот нет
lim_(x→+∞)f(x)=-∞;
lim_(x→-∞)f(x)=+∞.
Находим наклонную асимптоту.
k=lim_(x→∞)f(x)/x=lim_(x→∞)(17-x^2)/(4x^2-5x)=-1/4
b==lim_(x→∞)(f(x)-kx)=lim_(x→∞)(17-(5x/4))/(4x-5)=∞
4)f`(x)=(-2x*(4x-5)-4*(17-x^2))/(4x-5)^2=
=(10x-4x^2-68)/(4x-5)^2.
y`=0
10x-4x^2-68=0
уравнение не имеет корней, D < 0
Точек экстремума нет.
5)f``(x)=((10x-4x^2-68)/(4x-5)^2)=
=((10-8x)*(4x-5)^2-2(4x-5)*4*(10x-4x^2-68))/(4x-5)^4=
=(40x-32x^2-50+40x-80x+32x^2+544)/(4x-5)^3=
=+494/(4x-5)^3.
На (-∞;(5/4)) f``(x) < 0, функция выпукла вверх.
на((5/4);+∞)f``(x) > 0, функция выпукла вниз.
Точек перегиба нет.