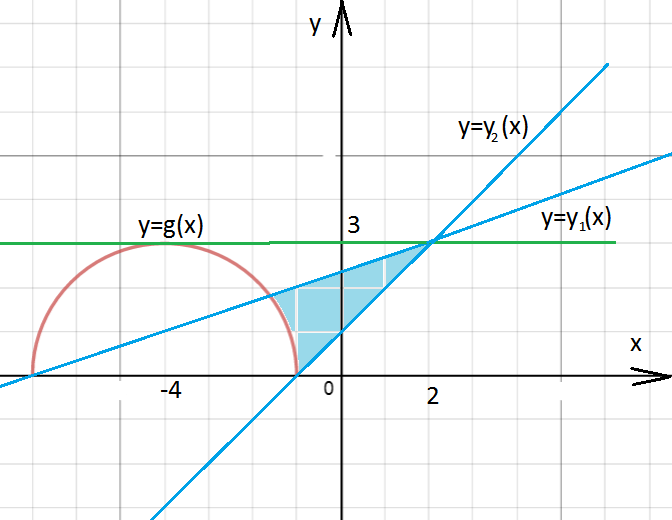
Задача 12414 Найдите все значение а, при каждом из...
Условие
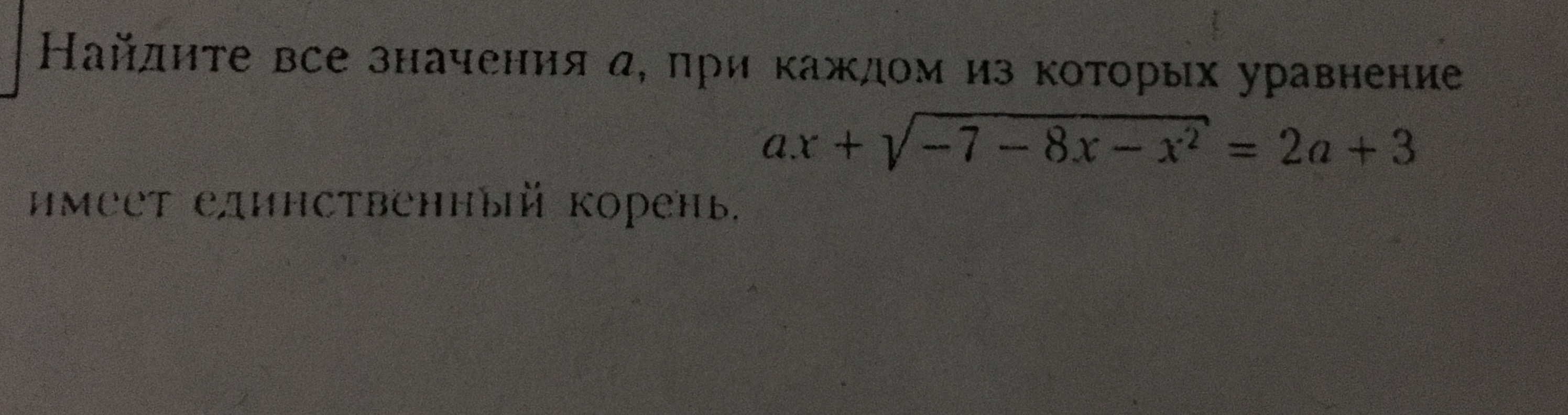
Решение
ax+y=2a+3
Решаем графически.
Сначала разберемся, что представляет из себя график функции
у=sqrt(-7-8x-x^2).
Возводим в квадрат
y^2=-7-8x-x^2
x^2+8x+y^2=-7
Выделяем полный квадрат
(х^2+2*4*x+16)+y^2=16-7
(x+4)^2+y^2=9 - уравнение окружности (-4;0) R=3
у=sqrt(-7-8x-x^2)- уравнение полуокружности, расположенной выше оси ох.
ax+y=2a+3
у=-a(х-2)+3 - пучок, семейство прямых, проходящих через точку (2;3).
Осталось найти угловые коэффициенты этих прямых
1) y=g(x)
а=0
2)у=у1(х)
Уравнение прямой, проходящей через точки (2;3) и (-1;0).
у=х+1
х+1=-а(х-2)+3⇒ а=-1
у=у2(х)- уравнение прямой проходящей через точки(2;3) и (-7;0)
у=(1/3)х+(7/3)
(1/3)х+(7/3)=-а(х-2)+3
а=-1/3
Все прямые, расположенные между у=у1(х) и у=у2(х) пересекаются с полуокружностью в одной точке.
О т в е т. [-1;-1/3)U{0}