Задача 12409 Решите log(6x^2-x-1)(2x^2-5x+3) больше...
Условие
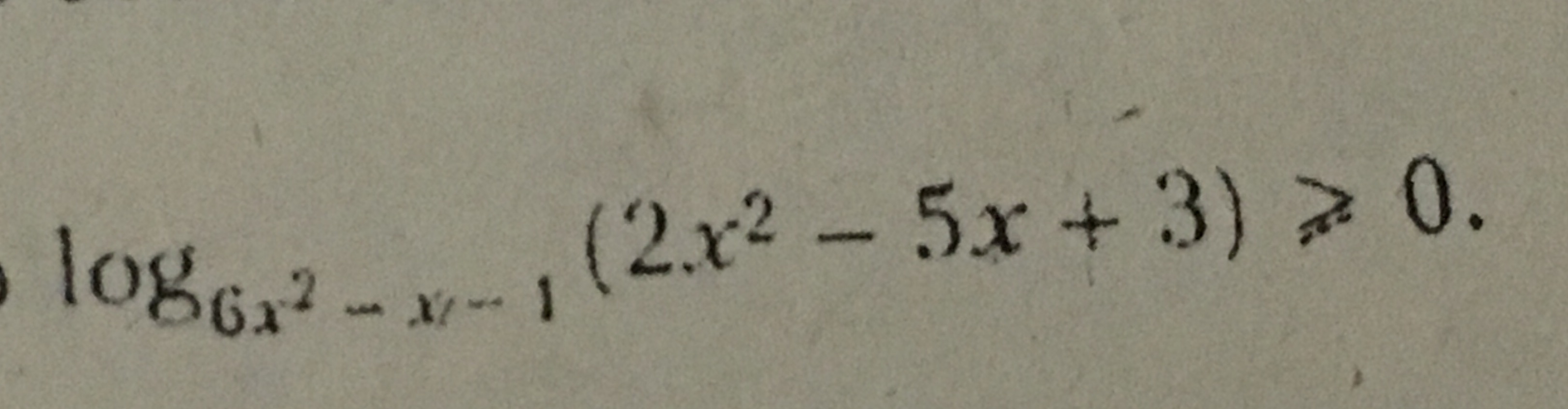
математика 10-11 класс
21510
Решение
★
{6x^2-x-1 > 0;6x^2-x-1≠1 ⇒6x^2-x-2≠0
{2x^2-5x+3 > 0.
Применяя метод рационализации логарифмических неравенств
(6х^2-x-1-1)*(2x^2-5x+3-1) больше или равно 0.
(6x^2-x-2)*(2x^2-5x+2)больше или равно 0.
Применяем метод интервалов
6x^2-x-2=0
D=1+48=49
x=-1/2 или х=2/3
x=-1/2 и х=2/3 отмечаем пустым кружком на числовой прямой ( cм. ОДЗ6x^2-x-2≠0)
2x^2-5x+2=0
D=25-16=9
x=2 или х=1/2
_+__ (-1/2) ____ [1/2] _+__ (2/3) ___ [2] _+_
О т в е т. (-бесконечность; -1/2)U[1/2;2/3)U[2;+ бесконечность)