Задача 12394 Диаметр окружности основания цилиндра...

Julia_Trusova

19.12.2016

Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно 7sqrt(10).

а) Постройте прямую пересечения этой плоскости с плоскостью, проходящей через диаметры оснований, перпендикулярные этим хордам.
б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.

а) Хорда длиной 24 находится на расстоянии sqrt(13^2-12^2)=5 от центра окружности основания, а хорда длиной 10 - sqrt(13^2-5^2)=12.
Поэтому расстояние между их проекциями на плоскость, параллельную основаниям, составляет либо 5+12=12, либо 12-5=7. Тогда расстояние между хордами составляет либо sqrt(21^2+17^2)=sqrt(730), либо sqrt(21^2+7^2)=sqrt(490)=7sqrt(10).
По условию задачи расстояние между хордами равно 7sqrt(10), то есть проекции хорд лежат по одну сторону от оси цилиндра.
Плоскость проходящая проходящей через диаметры оснований, перпендикулярные этим хордам будет пересекать эти хорды в их центрах(по свойству диаметра, перпендикулярного хорде).
Если О и О1 - центры оснований, АВ и А1В1 - хорды, Н и Н1 - центры этих хорд(см. рис.), то НН1 - прямая, по которой пересекаются плоскость АВА1В1 и плоскость, проходящая через диаметры оснований, перпендикулярные хордам.

б) Пусть Н1м-высота, опущенная из Н1.
Угол Н1НМ - линейный угол искомого двугранного угла.
НМ=ОН-О1Н1=12-5=7
Н1М=21(высота цилиндра)
Тогда, tgН1НМ=Н1М/НМ=21/7=3
Угол Н1НМ = arctg3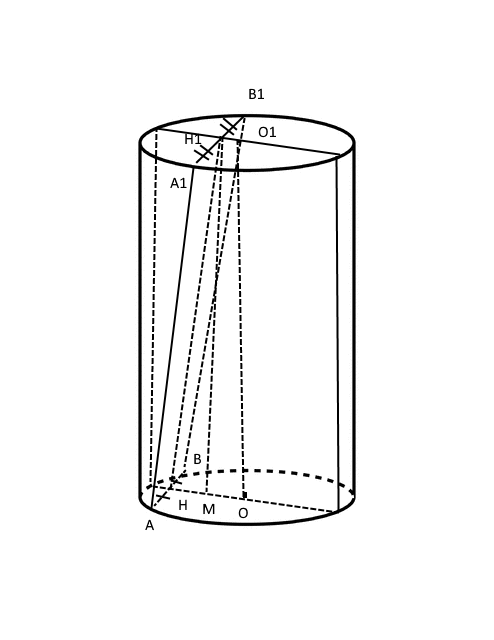

Ответ: б)arctg3