Задача 12357 Дана трапеция АВСD, основания которой...

Julia_Trusova

18.12.2016

Дана трапеция АВСD, основания которой ВС=44, AD=100, АВ=CD=35. Окружность, касающаяся прямых AD и АС, касается стороны CD в точке К.

а) Докажите, что АС=75.
б) Найдите длину отрезка СК.

СН-высота
Так как АВ=CD=35, то трапеция равнобедренная.
Тогда НD=(AD-BC):2=(100-44):2=28
AH=100-28=72
По теореме Пифагора из треугольника СDH:
CH=sqrt(CD^2-HD^2)=sqrt(35^2-28^2)=sqrt((35-28)(35+28))=sqrt(7*63)=21
По теореме Пифагора из треугольника АСН:
АС=sqrt(CH^2+AH^2)=sqrt(21^2+72^2)=sqrt(441+5184)=sqrt(5625)=75
Что и требовалось доказать.

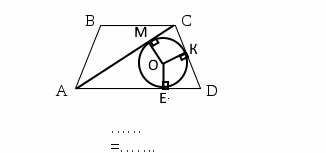
б) Так как окружность касается прямых AD и АС и касается стороны CD в точке К, возможны два случая(см. рис.).
Рассмотрим первый, если окружность вписана в треугольник АСD.
Теорема: В любом треугольнике расстояние от вершины треугольника до точки касания вписанной окружности со стороной треугольника, выходящей из данной вершины, есть разность полупериметра треугольника и стороны, противолежащей данной вершине.
Значит, СК=СМ=р-AD
p=(35+100+75)/2=105
CK=105-100=5

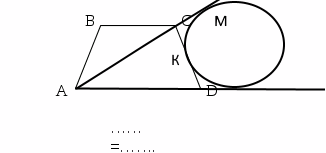
Рассмотрим второй случай, когда окружность касается прямых AD и АС и стороны CD с внешней стороны.
Теорема:В любом треугольнике расстояние от вершины треугольника до точки касания вневписанной окружности (касающейся противоположной данной вершине стороны треугольника и продолжений двух других его сторон) с продолжением стороны треугольника, выходящей из данной вершины, есть полупериметр треугольника.
Значит, АМ=р=105
СМ=СК
АМ=АС+СМ=АС+СК
СК=АМ-АС
СК=105-75=30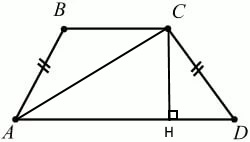

Ответ: 5 или 30