Задача 12346 Расстояние между центрами окружностей...

Julia_Trusova

18.12.2016

Расстояние между центрами окружностей радиусов 1 и 9 равно 17. Этих окружностей и их общей внутренней касательной касается третья окружность.

а)Докажите, что её точка касания с прямой совпадает с точкой касания одной из первых двух окружностей.

б)Найдите радиус третьей окружности.

а) Пусть х- радиус искомой окружности, О-её центр. СD-внутренняя касательная данных окружностей, О1 и О2 - их центры. Заметим, что прямая CD - либо общая внешняя касательная окружностей с центрами О и О2(см. рис.), либо окружностей с центрами О и О1(см. рис.). При этом её точка касания с прямой совпадает с точкой касания одной из первых двух окружностей, так как касательная будет проходить через общую точку(точку касания) окружностей.

б) Для нахождения радиуса третьей окружности, докажем сначала следующее утверждение. Если а-расстояние между центрами окружностей радиусов r и R, a⩾r+R, общая внешняя касательная касается окружностей в точках А и В, внутренняя в точках С и D, то
AB=sqrt(a^2-(R-r)^2), CD=sqrt(a^2-(R+r)^2).
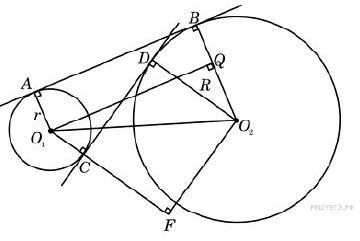
Действительно, пусть О1 и О2 -центры окружностей радиусов r и R соответственно(см. рис.2). Из точек О1 и О2 опустим перпендикуляры О1Q на прямую О2В и О2F на прямую О1С. Из прямоугольных треугольников О1QO2 и O1FO2 находим, что
O1Q=sqrt(O1O2^2-QO2^2)=sqrt(a^2-(R-r)^2), O2F=sqrt(O1O2^2-FO1^2)-sqrt(a^2-(R+r)^2).
Следовательно, CD=O2F=sqrt(a^2-(R+r)^2).
По доказанному CD=sqrt(17^2-(1+9)^2)=sqrt((17-10)(17+10))=sqrt(7*27)=3sqrt(21)

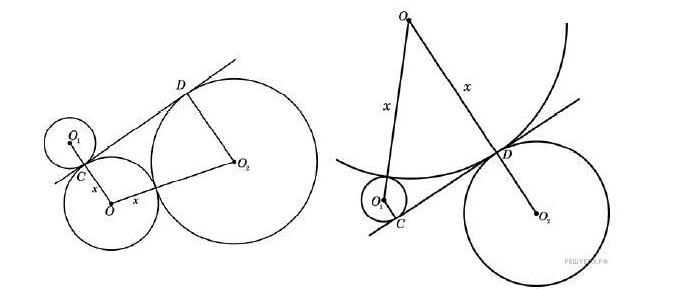
В первом случае CD-общая внешняя касательная к окружности с центрами О и О2, поэтому CD=sqrt((x+9)^2-(9-x)^2)=6sqrt(х)
6sqrt(х)=3sqrt(21)
2sqrt(х)=sqrt(21)
4х=21
х=5,25

Во втором случае CD-общая внешняя касательная к окружностям с центрами О и О1, поэтому CD=sqrt((x+2)^2-(2-x)^2)=2sqrt(х)
2sqrt(х)=3sqrt(21)
4x=189
x=47,25


Ответ: 5,25; 47,25