Задача 12339 ...
Условие
б)Найти корни, принадлежащие отрезку [π;5π/2]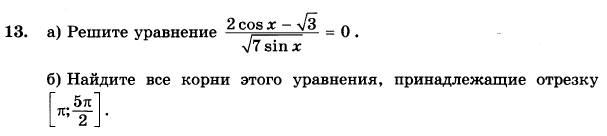
математика 10-11 класс
11337
Решение
x∈(2πk;π+2πk), k∈Z
2cosx-sqrt(3)=0
cosx=sqrt(3)/2
x= ± (π/6)+2πn, n∈Z
Учитывая ОДЗ
а) О т в е т. (π/6)+2πn, n∈Z
б) Составим неравенство
π меньше или равно (π/6)+2πn меньше или равно 5π/2,n∈Z
Вычитаем (π/6)
5π/6 меньше или равно 2πn меньше или равно 14π/6,n∈Z
Делим на π/6
5 меньше или равно 12n меньше или равно 14π, n∈Z
Неравенство верно при n=1
Значит х= (π/6) + 2π= 13π/6 - корень принадлежащий указанному промежутку
Ответ: а) (π/6)+2πn, n∈Z б) 13π/6.