Задача 1231 В сосуд, имеющий форму конуса, налили 50...
Условие
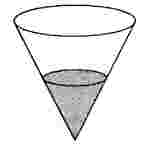
математика 10-11 класс
52194
Решение
V2 = (1/3)Pi(2R)^2h = 4*2*(1/3)PiR^2(h/2) = 8*V1 = 8*50 = 400 мл - объем большего конуса
V = V2-V1 = 400-50 = 350 мл
Ответ: 350
Все решения
Мы знаем,что отношение объемов подобных, тел равно кубу коэффициента подобия, поэтому
составляем отношение Vч/V=(1/2)^3. 50/V=1/8.Отсюда V=400 мл
Нужно долить 400-50=350(мл)
Ответ:350
