Задача 12300 Решите неравенство...
Условие
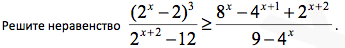
математика 10-11 класс
6364
Решение
★
2^x=t, t > 0
4^x=t^2
8^x=t^3
4^(x+1)=4t^2
2^(x+2)=4t
Неравенство принимает вид:
(t-2)^3/(4t-12) больше или равно (t^3-4t^2+4t)/(9-t^2);
((t-2)^3/(4t-12))+ (t(t^2-4t+4)/(t^2-9)) больше или равно 0;
(t-2)^2*(t+3+4t)/4*(t-3)*(t+3)больше или равно 0;
(t-2)^2*(5t+3)/4*(t-3)*(t+3)больше или равно 0;
_-___ (-3) ___+___ [-0,6]__-___[2]_-__ (3) __+__
-3 < t меньше или равно 0,6; t=2 ; t > 3
Так как t > 0, то 0 < t меньше или равно 0,6 ⇒ 2^x меньше или равно 0,6
⇒ х меньше или равно log_(2)0,6
2^x=2 ⇒ x=1
2^x > 3
x > log_(2)3
О т в е т.(-бесконечность; log_(2)0,6)U {1}U(log_(2)3; + бесконечность)