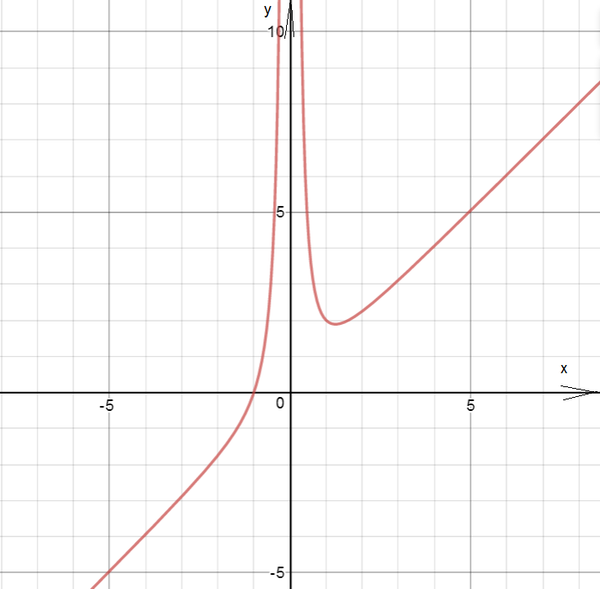
Задача 12226 Исследовать функции y= 1/3x^3-x^2-3x+1/3...
Условие
Решение
f(-0)=-бесконечность
f(+0)=+ бесконечность
х=0 - точка разрыва второго рода
х=0 - вертикальная асимптота.
2) Функция не является ни четной, ни нечетной.
у(-х)=(-х)^3+1/(-x)^2=(-x^3+1)/x^2
y(-x)≠y(x)
y(-x)≠-y(x)
3)lim_(x→ +бесконечность))f(x)=+бесконечность
lim_(x→-бесконечность)f(x)=-бесконечность.
4)
Наклонная асимптота
k=lim_(x→+бесконечность)(x^3+1)/x^3=1
b=lim_(x→+бесконечность)(f(x)-x)=lim_(x→+бесконечность)1/x^2=0
y=x- наклонная асимптота.
5) f(x)=0
x^3+1=0
x=-1
f(0)=не существует.
Точек пересечения с осью Оу нет.
6)y`=(3x^2·x^2–2x·((x^3+1))/(x^2)2;
y`=(3x^4–2x^4–2x))/(x^4);
y`=(x^3–2))/(x^3);
y`=0
x=∛2 – точка минимума, производная меняет знак с – на +
Знак производной:
___–____ (0) __–__ (∛2 ) __+__
у убывает у убывает у возрастает
у(∛2)=(2+1)/∛4=3/∛4
7)y``=((x^3-2)/x^3)`=(1-(2x^(-3))`=(6/x^4) > 0
при всех х≠0
Функция выпукла вниз
Точек перегиба нет.