Задача 12185 ...

SOVA

13 декабря 2016 г.

В правильной треугольной призме АВСA1B1C1 все ребра равны между собой.

Точка К – середина ребра СС1. Докажите, что прямые АВ1 и ВК перпендикулярны.

Достроим треугольную призму АВСA1B1C1 до четырехугольной АВСDA2B2C2D2.
В основании ромб ABCD с острым углом 60 °.
Боковое ребро АА2=2·АА1
Прямые АВ1 и ВК – скрещивающиеся.
Через одну из скрещивающихся прямых АВ1 проводим плоскость параллельную ВК.
В1F||BK
AE||BК
АЕ=B1F
AEFB1– параллелограмм.
Пусть ребро данной призы равно а.
Из прямоугольного треугольника АСF по теореме Пифагора
AF²=AC^+CF²=a^+(3a/2)²=13a²/4.
Из прямоугольного треугольника АBB1 по теореме Пифагора
AB²₁=AB^+BB²₁=a^+a²=2a².
Из прямоугольного треугольника BСK по теореме Пифагора
BK²=BC^+CK²=a^+(a/2)²=5a²/4.
BK=B1F
В треугольнике АB1F:
AF²=AB²₁+B1F²
13a²/4=2a²+(5a²/4)– верно.
По теореме обратной теореме Пифагора
треугольник АВ1F– прямоугольный.
АВ1 ⊥ В1F, а значит АВ1⊥ ВК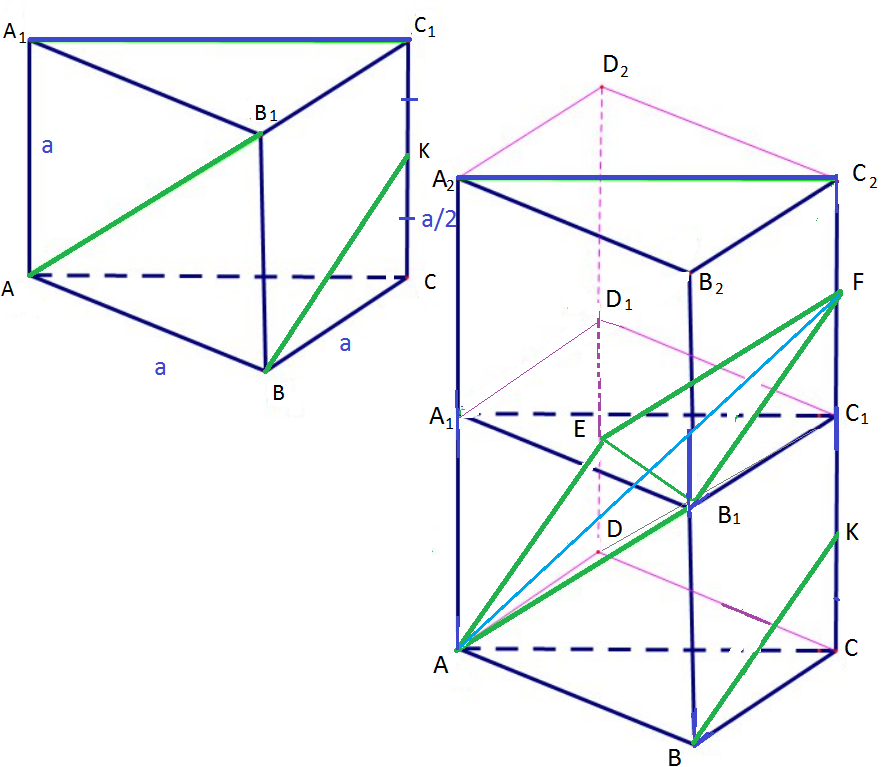

Ответ: В решение