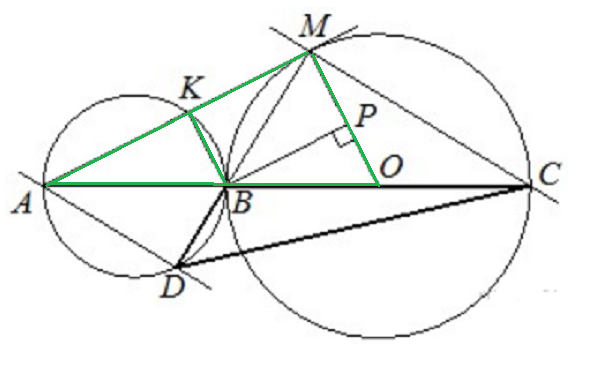
Задача 12100 Точка B лежит на отрезке AC. Прямая,...

slava191

09.12.2016

Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.

а) Докажите, что прямые AD и MC параллельны.

б) Найдите площадь треугольника DBC, если AK=3 и MK=12.

SOVA

09.12.2016

★

A) Точки М и D лежат на окружностях с диаметрами ВС и АВ.
∠ ВМС=∠BDA=90 градусов
Прямые МС и AD перпендикулярны одной и той же прямой MD,значит они параллельны.
МС||AD.
Б) Пусть О- центр окружности с диаметром ВС.
ОМ ⊥ АМ
Так как ВК ⊥ АМ, то ОМ||ВК.
Пусть ВК=х
Треугольники АМО и АВК подобны, коэффициент подобия равен 5 (АК=3; АМ=АК+КМ=3+12=15)
ОВ=ОМ=5х

BP⊥ OM,
КМРВ-прямоугольник.
ВР=КМ=12
ОР=ОМ-МР=ОМ-ВК=5х-х=4х
По теореме Пифагора
ОВ^2=ВР^2+ОР^2
(5х)^2=12^2+(4x)^2;
25x^2=144+16x^2
9x^2=144
x^2=16
x=4

S(ΔMDC)=S(ΔMAC)
Основание у этих треугольников общее – МС.
Высота тоже общая, высота– расстояние между параллельными прямыми AD и МС
А если от равных площадей отнять площадь треугольника МВС, то оставшиеся части также будут равны.
S(ΔMDC)–S(ΔMBC)=
=S(ΔMAC)–S(ΔMBC).

S(Δ DBC)=S(ΔMDC)-S(ΔMBC)=
=S(ΔMAC)-S(ΔMBC)=S(ΔABM)

S(Δ DBC)=S(ΔABM)=AM*BK/2=15*4/2=30

О т в е т. 30