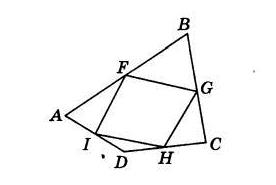
Задача 12008 Дан выпуклый четырёхугольник АВСD. На...

Julia_Trusova

02.12.2016

Дан выпуклый четырёхугольник АВСD. На стороне АВ взяли точку F, на стороне ВС - точку G, на стороне CD - точку Н, на стороне AD - точку I. Докажите, что периметр четырехугольника FGHI меньше периметра четырёхугольника ABCD.

P(ABCD)=AB+BC+CD+AD=AF+FB+BG+GC+CH+HD+DI+IA
P(IFGH)=IF+FG+GH+HI
Из треугольника AFI: FI < AF+AI(сторона треугольника меньше суммы двух других его сторон)
= > FG < BF+BG
GH < GC+CH
IH < DH+DI
Значит, P(IFGH) < P(ABCD)

Ответ: В решение