Задача 11963 В окружности радиуса 13 проведены...

Julia_Trusova

30.11.2016

В окружности радиуса 13 проведены касательная и параллельная её хорда, расстояние между которыми равно 18. Найдите длину хорды.

ОМ=ОВ=r=13 (так как радиус проведен в точку касания, он перпендикулярен касательной)
Так как расстояние между касательной и хордой больше радиуса, то центр окружности будет находиться между касательной и хордой, то есть ОМ=13, тогда ОН=18-13=5
Так касательная и хора АВ параллельны, то диаметр, проходящий через радиус ОМ так же перпендикулярен и хорде АВ, а значит, Н-середина АВ
По теореме Пифагора из треугольника ОНВ:
НВ=sqrt(13^2-5^2)=sqrt(169-25)=sqrt(144)=12
Тогда АВ=2*НВ=2*12=24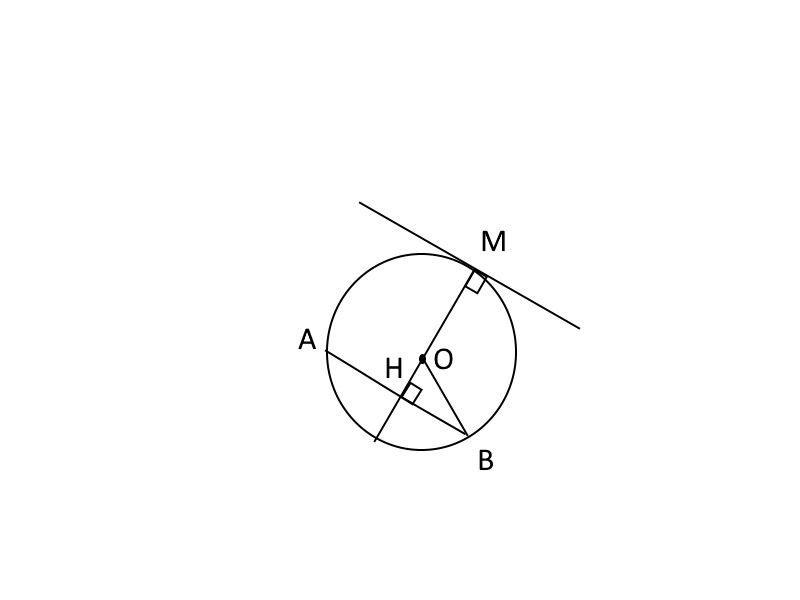

Ответ: 24