Задача 11962 Постройте график функции...

Julia_Trusova

30.11.2016

Постройте график функции у=(3х^3+x^2)/(3x+1) и определите, при каких значениях с прямая у=с будет иметь с построенным графиком не более одной общей точки.

у=(3х^3+x^2)/(3x+1)
ОДЗ: 3х+1≠0
3х≠-1
х≠-1/3 (при этом значении х, точки на графике будут выколотые)
у=(3х^3+x^2)/(3x+1)
у=x^2(3х+1)/(3x+1)
y=x^2 - квадратичная функция, графиком является парабола, ветви направлены вверх(a > 0), вершина параболы имеет координату (0;0).
Графиком функции у=(3х^3+x^2)/(3x+1) будет являться парабола y=x^2 с выколотой точкой х=-1/3 (при х=-1/3, у=(-1/3)^2=1/9)
При с=1/9 и с⩽0 прямая у=с будет иметь с построенным графиком не более одной общей точки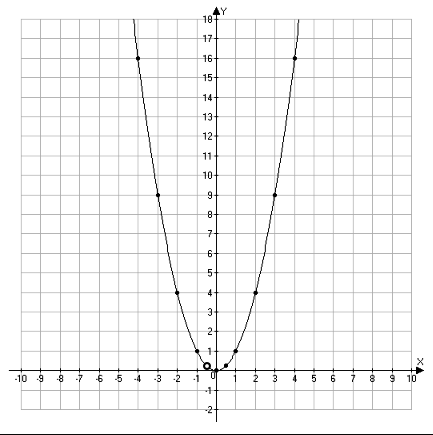

Ответ: с⩽0, с=1/9