Задача 1187 Биссектриса угла ADC параллелограмма...

slava191

16.05.2014

Биссектриса угла ADC параллелограмма ABCD пересекает прямую AB в точке E. В треугольник ADE вписана окружность, касающаяся стороны AE в точке K и стороны AD в точке T.
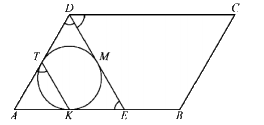
а) Докажите, что прямые KT и DE параллельны.
б) Найдите угол BAD, если известно, что AD = 6 и KT = 3.

а) Угол AED = углу CDE (накрест лежащие при AB || DC)
Угол CDE = углу ADE (DE - биссектриса)
Значит угол ADE= углу AED и треугольник DAE - равнобедренный AD=AE
Треугольник ATK также равнобедренный AT=TK. Угол A - общий, значит треугольники подобны и угол ATK = углу ADE из чего следует, что TK||DE
б) AT/DE=TK/DE
Пусть DT=DM=x, тогда (6-x)/6=3/2x
x=3
DE=2x=6. Значит ADE - равносторонний и угол BAD= углу EAD=60 градусов


Ответ: 60 градусов