Задача 1186 В треугольник ABC вписана окружность...

slava191

16.05.2014

В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причем AD=R.
a) Докажите, что треугольник ABC прямоугольный.
б) Вписанная окружность касается сторон AB и BC в точках E и F. Найдите площадь треугольника BEF, если известно, что R=5 и CD=15.

а) OD перпендикулярно CA, значит угол ODA=90 градусов
ОЕ=ОВ=DA=ЕО=R, значит OEAD - квадрат, следовательно угол EAD=углу CAB=90 градусов, ч.т.д.
б) Пусть BE=x=BF, тогда по теореме Пифагора
20^2=(15+x)^2-(5+x)^2
x=10
sinABC=AC/BC=4/5
S=(1/2)*BF*BE*sinABC=40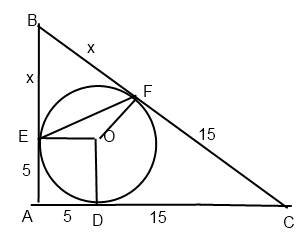

Ответ: 40