Задача 11836 ...

slava191

26.11.2016

В основании прямой призмы АВСDA1B1C1D1 лежит равнобедренная трапеция АВСD с основаниями ВС и АD. Точка К – середина ребра ВВ1. Плоскость α проходит через середины ребер АВ и ВВ1 параллельно прямой В1D.

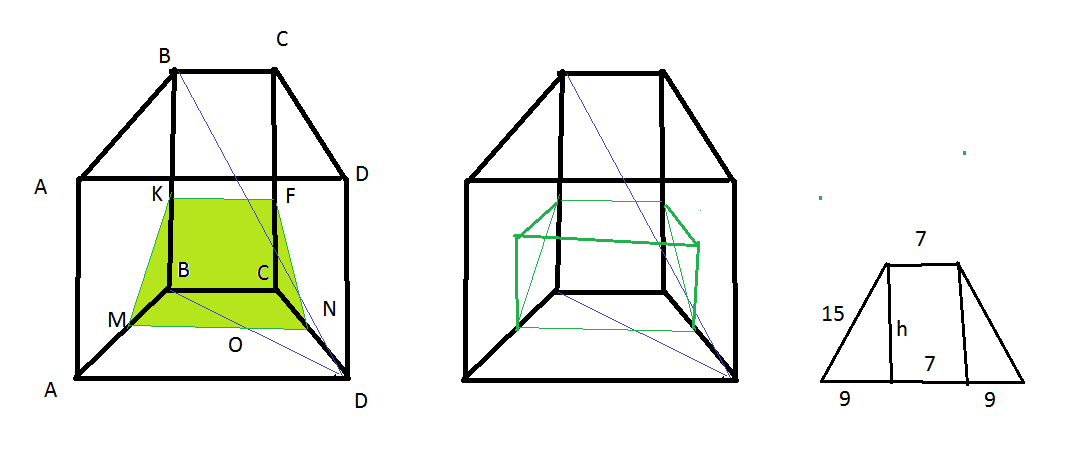
А) Докажите, что сечением призмы плоскостью α является равнобедренная трапеция.

Б) Найдите объем большей части призмы, на которые ее разбивает плоскость α, если известно, что ВС=7, АD=25, АВ=15, ВВ1=8.

SOVA

26.11.2016

★

Пусть М- середина АВ, АМ=МВ.
В треугольнике ВВ1D проводим КО || B1D.
Так как ВК=КВ1, КО- средняя линия треугольника ВВ1D.
BO=OD.
МО - средняя линия треугольника АВD,
MO||AD, AD||BC, значит МО||ВС.
MN-средняя линия трапеции АВСD.
CN=ND.
КF||BC, KF=BC,
C1F=FC.
KF||MN, значит ABCD- трапеция.

Грани AA1B1B и СС1D1D- равны. AA1=BB1=CC1=DD1.
AB=CD.
Значит и диагонали этих граней равны. АВ1=DC1
MK=AB1/2=DC1/2=FN
Cечение МКFN - равнобедренная трапеция.

Б) h(трапеции)=sqrt(15^2-9^2)=12
MN=(BC+AD)/2=(7+25)/2=16

V(призмы АВСВА1В1С1D1)=S(трапеции АВСD)*H=
=((7+25)*12/2)*8=1536 куб.ед.

v(меньшей части)=1/2 V1
V1-объем прямой призмы с основанием МВСN и высотой КВ=Н/2.
V1=((BC+MN)*h/2)/2(*H/2)=((7+16)*6/2)*4=276
v=276/2=138 куб.ед.

V(большей части)=V(призмы АВСВА1В1С1D1)-v(меньшей части)=1536-138=1398 куб.ед
О т в е т. 1398 куб. ед.