Задача 11805 При каком значении параметра а уравнение...
Условие
|x^2-3ax|=a
имеет три корня?
математика 10-11 класс
3900
Решение
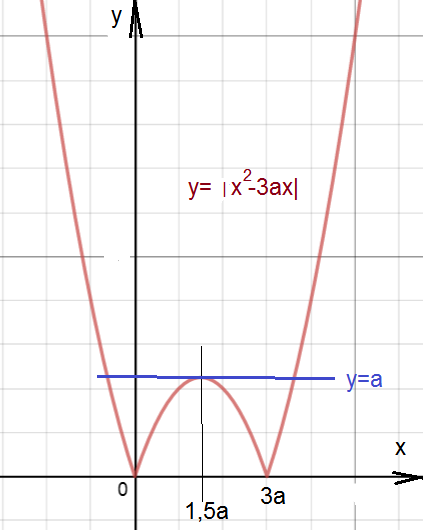
то a > 0 ( при а=0 один корень).
Количество корней уравнения - это количество
общих точек графика функции
у=|x^2-3ax| и горизонтальной прямой у=а.
Из рисунка видно, что уравнение будет иметь
три точки пересечения в том случае, если
горизонтальная прямая у=а будет проходить
через точку локального максимума функции
у=|x^2-3ax|.
х_(в)=1,5а
у_(в)=|(1,5a)^2-3a*1,5a|=|-2,25a^2|=2,25a^2
Из уравнения
2,25а^2=a
а≠0 получаем
а=1/2,25=4/9
Ответ: 4/9