Задача 11783 Две окружности касаются внутренним...

slava191

23 ноября 2016 г.

Две окружности касаются внутренним образом в точке Т. Хорда АВ внешней окружности касается внутренней окружности в точке S. Прямая TS пересекает внешнюю окружность в точках Т и С. Найдите площадь четырёхугольника ТАСВ, если известно, что СВ = ВТ = 3, а радиусы окружностей относятся как 5 : 8.

SOVA

24 ноября 2016 г.

★

Пусть k – коэффициент пропорциональности радиусов, тогда R=8k; r=5k.
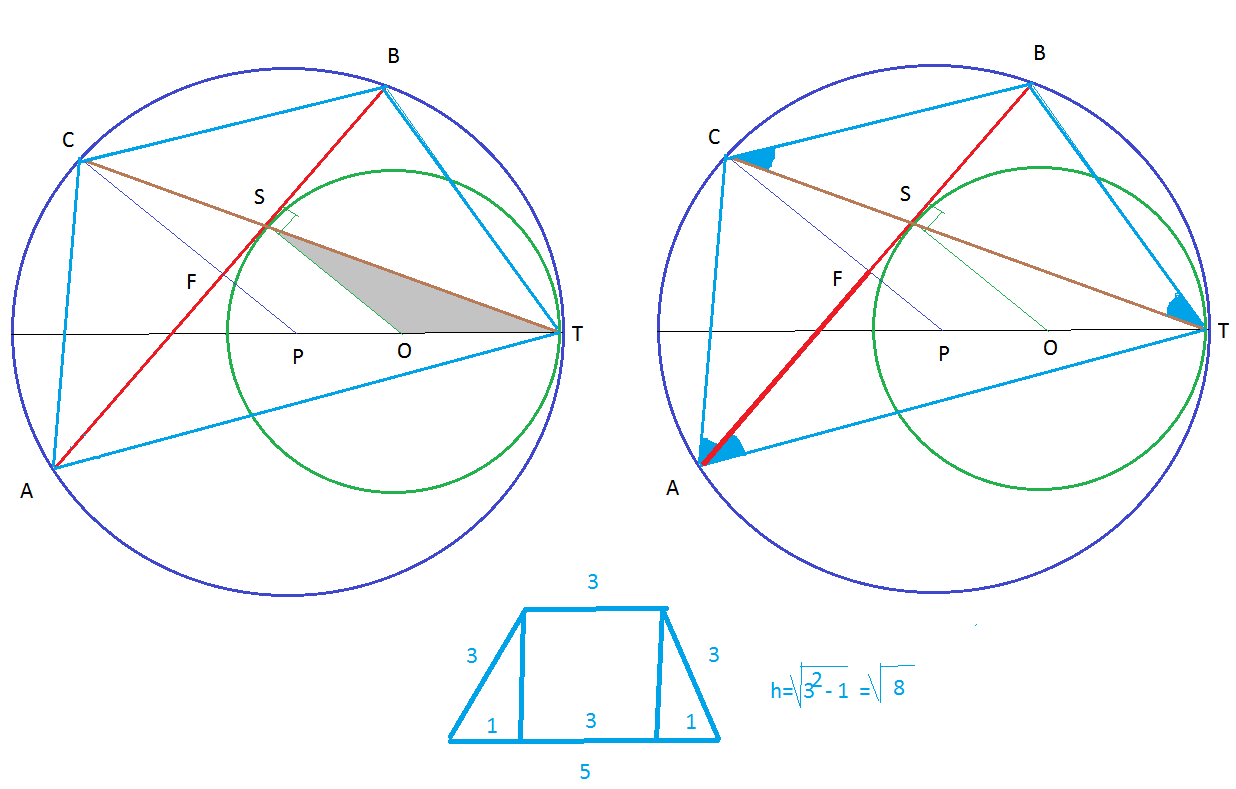
O–центр окружности радиуса 5k, Р– центр окружности радиуса 8k.
Точки О,Р,Т лежат на одной прямой.
SO=OT=5k
CP=PT=8k
Равнобедренные треугольники SOT и СРТ подобны, угол СТО– общий.
РТ=РО+ОТ
8k=PO+5k⇒ PO=3k
OT:TP=TS:TC=5k:8k=5:8,
TS:CS=TO:OP=5:3 ( по теореме Фалеса) или
СS:ST=3:5

SO⊥AB
CP || SO, значит СР || SO и СP⊥AB
CP– диаметр.
Диаметр перпендикулярный хорде делит хорду пополам.
AF=FB.
CF– высота и СF– медиана, треугольник АСВ – равнобедренный АС=СВ.

По условию ВС=ВТ, равные хорды стягивают равные дуги.

∠САВ=∠ВАТ=∠СТВ=∠ВСТ как углы опирающиеся на равные дуги.
и
∠СВА=∠СТА ( доказано, АС=ВС)

Значит, АВ– биссектриса угла А и
по свойству биссектрисы угла треугольника САТ
СS:ST=CA:АТ
По доказанному ранее
СS:ST=3:5
значит
СА:АТ=3:5
и так как СА=3, значит АТ=5

∠САВ=∠ВАТ, внутренние накрест лежащие углы и значит
ВС||AT.

Четырехугольник ТАСВ – равнобедренная трапеция.
h=√3²–1=sqrt(80
S(трапеции)=(ВС+АТ)·h/2=(3+5)·√8/2=4√8=8√2
О т в е т. S(TABC)=8√2

u37110210148

7 июня 2017 г. в 00:00

Решение от МГУ