Задача 1172 На клетчатой бумаге с размером клетки...

slava191

15.05.2014

На клетчатой бумаге с размером клетки 1x1 отмечены точки A и B. Найдите длину отрезка AB.

Что может быть проще, чем просто посчитать клеточки и подставить цифры в теорему Пифагора:
L^2=15^2+8^2
L=sqrt(289)=17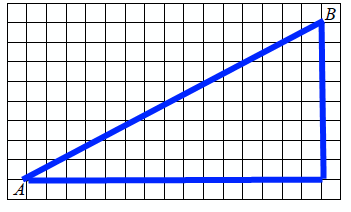

Ответ: 17

Гость

23.12.2014

через теорему Пифагора.
Можно ввести дополнительную точку С так, чтобы получился прямоугольный треугольник АВС.
потом посчитать клетки: длина АС=8кл.,ВС=15 кл.
чтобы найти АВ воспользуемся теоремой:
АВ2=АС2+ВС2 (всё в степени 2)
АВ2=289
АВ=17
17кл.= 85 мм = 8.5 см
Не знаю,что именно в ответе указывать :(